Osebne zbirke


Naravna števila so števila, s katerimi štejemo: 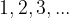
Množico naravnih števil označimo s črko 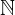 :
:
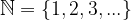
Številska premica je črta, ki je na levi strani omejena s točko, ki označuje izhodišče - število 0. Na desni strani pa se razteza v neskončnost:

Števila na premici označimo s točkami, ki so med seboj enakomerno oddaljene. Razdaljo med posameznimi točkami imenujemo enota. Enota je poljubne dolžine, vedno pa mora biti enaka med vsemi števili. Določimo jo med točkama 0 in 1. Potem jo nanašamo naprej po osi, da dobimo še druga naravna števila.
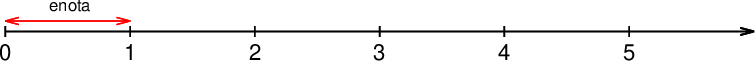
Število 0 ne spada med naravna števila.
Na številski premici naj bosta vedno označeni števili 0 in 1, ostala števila pa zapišemo po potrebi.
Razvrstitev števil po velikosti si najlažje ogledamo na številski premici. Velja preprosto pravilo: števila naraščajo od leve proti desni. Tako je poljubno število večje od vseh, ki od njega ležijo levo.
Za naravna števila velja:
Najmanjše izmed danih števil je na številski premici prikazano najbolj levo, največje število pa najbolj desno.
Zgornjo trditev lahko zapišemo tudi drugače:
Večje število na številski premici vedno leži desno od manjšega.
Če se po številski premici premikamo v levo stran, se vrednost manjša (negativna sprememba), če se premikamo desno, pa se veča (pozitivna sprememba).
Pri razlagi računskih operacij seštevanja in odštevanja z naravnimi števili si bomo pomagali s številsko premico, na kateri števila naraščajo od leve proti desni.
Če neko število povečamo, se premakne v desno stran, če pa ga zmanjšamo, se premakne v levo stran.
Naravnemu številu a prištejmo naravno število b.
Na številski premici si izberimo naravno število a:

Če temu številu prištejemo naravno število, se mu vrednost poveča, zato se premakne v desno. Tudi vsota se nahaja desno od števila 0:

Vsota števil je od izhodišča številske premice oddaljena toliko kot seštevek posameznih števil.
Če seštejemo poljubni naravni števili, vedno dobimo naravno število, ki je večje od posameznega seštevanca.
Sedaj pa od naravnega števila a odštejmo naravno število b.
Na številski premici si izberimo naravno število a:

Če od tega števila odštejemo naravno število b, se mu vrednost zmanjša, zato se premakne v levo:

Prikaz situacije, ko je število b manjše od števila a.
Če od naravnega števila a odštejemo naravno število b, pri čemer velja 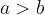 , dobimo naravno število, ki je manjše od zmanjševanca.
, dobimo naravno število, ki je manjše od zmanjševanca.
Če od naravnega števila a odštejemo naravno število b, pri čemer velja 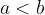 , potem rezultat ni naravno število.
, potem rezultat ni naravno število.
Tudi pri razlagi računskih operacij množenja in deljenja z naravnimi števili si bomo pomagali s številsko premico.
Vemo, da na številski premici števila naraščajo od leve proti desni. Za vsako prišteto naravno število se pomaknemo za določeno število mest v desno.
Množenje naravnih števil pa si lahko predstavljamo kot neko "večkratno seštevanje" oziroma štetje z enakomernimi skoki, kar na številski premici pomeni večkratni pomik za enako število mest v desno.
Rezultat množenja pa je lahko tudi enak enemu od faktorjev.
Če zmnožimo poljubni naravni števili, vedno dobimo naravno število, ki je večje ali enako od posameznega faktorja.
Ogledali si bomo dva načina predstavljanja deljenja na številski premici:
kot večkratno odštevanje enakega števila od določene vrednosti in
kot razdelitev določene razdalje od izhodišča na enake dele.
Prvi način:
Vemo, da na številski premici števila naraščajo od leve proti desni. Za vsako odšteto naravno število se pomaknemo za določeno število mest v levo.
Deljenje naravnih števil pa si lahko predstavljamo kot neko "večkratno odštevanje" oziroma štetje z enakomernimi skoki, kar na številski premici pomeni večkratni pomik za enako število mest v levo.
Deljenje pa se lahko tudi ne izide.
Drugi način:
Deljenje si na številski premici lahko predstavljamo tudi kot razdelitev določene razdalje od izhodišča na enake dele.
Oglejmo si ga na enakih primerih kot prej.
Kadar dolžina posameznega dela ni enaka večkratniku enote, se deljenje ne izide in rezultat ni naravno število.
Če naravno število a delimo z naravnim številom b, pri čemer je a večkratnik b, dobimo naravno število, ki je manjše ali enako od deljenca.
Če naravno število a delimo z naravnim številom b, pri čemer a ni večkratnik b, potem rezultat ni naravno število.