Prijava z e-naslovom
Prijava brez gesla
Z množico označujemo skupino različnih elementov. Elementi množice so lahko števila, črke, vozila, sadje itd., ki jih združimo v množico in jih povezuje neka skupna lastnost.
Množica je skupina elementov, ki jih druži določena lastnost. Označimo jo z velikimi tiskanimi črkami:
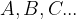
njene elemente pa zapišemo v zavite oklepaje.
Vsako posamezeno enoto množice imenujemo element množice.
Če množica A vsebuje element a, to zapišemo s simboli:
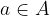
in beremo: a je element množice A.
Če množica A ne vsebuje elementa x, to zapišemo kot:
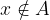
in beremo: x ni element množice A.
Če množica A ne vsebuje nobenega elementa, to zapišemo s simboli:
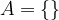
ali
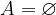
in pravimo, da je A prazna množica.
Množice delimo na:
končne (imajo končno mnogo elementov)
neskončne (imajo neskončno mnogo elementov)
Univerzum ali univerzalna množica je množica iz katere izbiramo elemente. Lahko je končna ali neskončna množica.
Podmnožica ali delna množica množice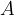 
je taka množica 
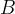, če je vsak element množice 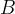vsebovan tudi v množici 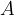. Množico B, ki je podmnožica množice A, označimo z:
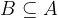
ali
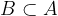
Potenčna množica množice 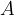je množica vseh njenih podmnožic. Elementi potenčne množice so torej množice. Potenčno množico množice A označimo z:
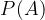
Množici 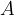in 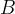sta enaki, če je množica 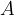podmnožica množice 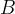, hkrati velja, da je tudi množica 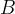podmnožica množice :
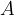Moč množice je število elementov, ki jih množica vsebuje. Oznaka je:
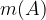
in beremo: moč množice A.
Dodajmo še trditve:
Če ima množica A n elementov, je moč njene potenčne množice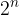 
.
Moč unije množic A in B je enako vsoti moči obeh množic, od katere odštejemo moč preseka množic (število elementov, ki so vsebovani tako v A kot v B):
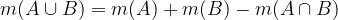
Če ima neka množica 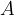toliko elementov, kot je naravnih števil, pravimo da je števno neskončna. Njena moč je alef nič (prva črka hebrejske abecede):
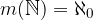
Množice ponazarjamo z Vennovimi diagrami. Univerzum ali univerzalno množico označimo s pravokotnikom, množice pa s sklenjenimi krivuljami.
Vennov diagram
