Osebne zbirke


Vsak par naravnih števil ima vsaj enega skupnega delitelja, to je število 1.
Skupni delitelji dveh števil 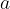 in
in 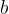 so število 1, skupni prafaktorji ter vsi možni produkti skupnih prafaktorjev, v kolikor le ti obstajajo.
so število 1, skupni prafaktorji ter vsi možni produkti skupnih prafaktorjev, v kolikor le ti obstajajo.
Največji skupni delitelj dveh števil 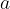 in
in 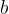 , je največji izmed deliteljev, ki delijo obe števili.
, je največji izmed deliteljev, ki delijo obe števili.
Označimo ga z
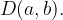
Največji skupni delitelj dobimo kot produkt vseh skupnih prafaktorjev, vključno z večkratnostmi.
Iščemo lahko tudi skupne delitelje večih števil. Tedaj je največji skupni delitelj produkt vseh skupnih prafaktorjev vseh števil.
Vsaki dve naravni števili imata neskončno skupnih večkratnikov.
Najmanjši skupni večkratnik dveh števil 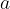 in
in 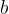 je najmanjše število, ki je deljivo z obema številoma
je najmanjše število, ki je deljivo z obema številoma 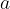 in
in 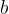 .
.
Označimo ga z
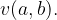
Najmanjši skupni večkratnik izračunamo s pomočjo razcepa na prafaktorje, pomnožimo namreč vse potence prafaktorjev z največjim eksponentom, ki jih najdemo v razcepu vsaj enega izmed števil.
Za iskanje največjega skupnega delitelja lahko uporabimo tudi računski postopek, ki mu rečemo Evklidov algoritem. Največji skupni delitelj je zadnji ostanek v algoritmu, ki je različen od 0. V postopku Evklidovega algoritma na vsakem koraku uporabljamo osnovni izrek o deljenju 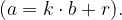
Poglejmo na primerih.