Osebne zbirke


Naravna števila so števila s katerimi štejemo. Množico naravnih števil označimo z 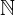 in jo sestavljajo števila od ena do neskončno, kar označimo kot:
in jo sestavljajo števila od ena do neskončno, kar označimo kot:
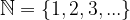
Lastnosti so:
naravnih števil je neskončno mnogo
1 je naravno število
vsako naravno število 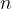 ima svojega naslednika
ima svojega naslednika 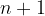
dve različni naravni števili 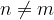 imata različna naslednika
imata različna naslednika 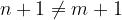
1 ni naslednik nobenega naravnega števila
Izberemo si izhodišče in enoto - izhodišče označimo z 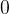 in eno enoto v desno število
in eno enoto v desno število 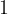
eno enoto v desno od števila 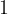 dobimo število
dobimo število 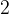
postopek ponavljamo, tako da enakomerno nanašamo enoto v desno in tako dobimo še ostala števila 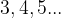
V množici naravnih števil sta definirani operaciji seštevanja in množenja.
Poljubni dve naravni števili 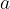 in
in 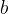 seštejemo in dobimo vsoto
seštejemo in dobimo vsoto 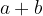 , pri čemer števili
, pri čemer števili 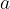 in
in 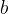 imenujemo seštevanec,
imenujemo seštevanec, 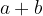 pa vsota.
pa vsota.
Poljubni dve naravni števili 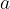 in
in 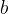 zmnožimo in dobimo zmnožek oziroma produkt
zmnožimo in dobimo zmnožek oziroma produkt 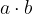 , pri čemer števili
, pri čemer števili 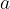 in
in 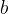 imenujemo zmnoženec oziroma faktor,
imenujemo zmnoženec oziroma faktor, 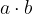 pa zmnožek oziroma produkt.
pa zmnožek oziroma produkt.
Pri računanju z naravnimi števili moramo upoštevati vrstni red operacij (množenje ima prednost pred seštevanjem) in oklepaje, zraven tega pa za računanje z naravnimi števili veljajo določeni zakoni.
Rezultat je neodvisen od vrstnega reda seštevanja oziroma množenja.
Komutativnost seštevanja:
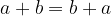
Komutativnost množenja:
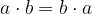
Rezultat je neodvisen od vrstnega reda združevanja faktorjev.
Asociativnost seštevanja:
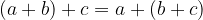
Asociativnost množenja:
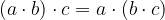
Povezuje množenje in seštevanje naravnih števil.
Distributivnost:
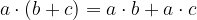
Pri množenju z 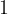 se rezultat ne spremeni.
se rezultat ne spremeni.
Nevtralni element za množenje:
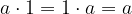
Praštevilo je naravno število, ki ima natanko dva delitelja 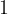 in samega sebe. Vsa ostala naravna števila, ki imajo več kot dva delitelja imenujemo sestavljena števila. Izjema je število
in samega sebe. Vsa ostala naravna števila, ki imajo več kot dva delitelja imenujemo sestavljena števila. Izjema je število 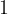 , ki ima samo enega delitelja, zato ni sestavljeno, niti praštevilo.
, ki ima samo enega delitelja, zato ni sestavljeno, niti praštevilo.
Vsako naravno število lahko na en sam način razcepimo na prafaktorje (praštevila) oziroma zapišemo kot produkt potenc s praštevilskimi osnovami:
Razcep naravnega števila n na prafaktorje (praštevila):
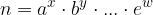
kjer so 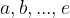 praštevila;
praštevila; 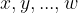 pa eksponenti, ki so naravna števila.
pa eksponenti, ki so naravna števila.
Izpostaviti skupni faktor pomeni, da pred oklepaj zapišemo največ, kar imajo vsi členi skupnega. Števila najprej razcepimo na produkt prafaktorjev (praštevil). Faktorje, ki jih vsebujejo vsi členi zapišemo pred oklepaj, vse kar nam od členov ostane, pa zapišemo v oklepaj.