Prijava z e-naslovom
Prijava brez gesla
Oglejmo si primer obrestovanja, ki ga pogosto srečamo v vsakdanjem življenju.
Vsebina zgornjega primera nam je zagotovo znana iz vsakdanjega življenja, uporabljena terminologija pa nam je morda tuja. Zato si oglejmo razlago uporabljenih izrazov.
Znesek kredita imenujemo glavnica ali kapital. Označimo jo z oznako G.
Znesek, ki ga moramo odplačati poleg glavnice, imenujemo obresti. Označimo jih z oznako o.
Obrestna mera je v odstotkih izražen znesek, ki ga po nekem obdobju obrestovanja pripišemo glavnici. Označimo jo z oznako p.
Običajno obrestujemo z letno obrestno mero, kar pomeni, da glavnici pripišemo obresti po zaključku vsakega leta.
Obrestovalna doba imenujemo obdobje, v katerem se nam na glavnico pripišejo obresti. Označimo jo s črko m ali n.
To obdobje je najpogosteje enako enemu letu, polovici leta ali enemu mesecu.
Letno obrestovalno dobo imenujemo tudi osnovna obrestovalna doba ali kapitalizacijska doba.
Če je obrestovalna doba krajša od enega leta, je njena osnovna enota dan ali mesec:
Če je osnovna enota dan, nam v navadnem letu dan predstavlja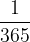 
letne obrestovalne dobe, v prestopnem letu pa 
.
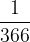Če je osnovna enota mesec, potem mesec predstavlja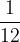 
letne obrestovalne dobe.
Vsako varčevanje ali odplačevanje kredita se po določenem času izteče ali zaključi.
Celotno odplačevalno obdobje imenujemo čas obrestovanja, in je obdobje, v katerem se znesek obrestuje.
Ko si nek znesek izposodimo od finančne ustanove, govorimo o tem, da vračamo dolg, ki je sestavljen iz:
dejanskega zneska, ki smo ga dobili (glavnice)
ter obresti, ki jih plačamo, zato da smo si ta denar lahko izposodili.
Ko znesek vložimo v finančno ustanovo, govorimo o vlogi. Znesek, ki ga dobimo po določenem obdobju, je sestavljen iz:
dejanskega zneska, ki smo ga vložili (glavnice)
ter obresti, ki nam jih je dala finančna ustanova, zato ker smo pri njih vložili svoj denar.
Višina obresti je vedno odvisna od naslednjih faktorjev:
glavnice ali začetnega kapitala
časa obrestovanja
obrestne mere
S takim denarnim poslovanjem se v vsakdanjem življenju pogosto srečujemo, ko varčujemo, najemamo in odplačujemo kredit, ustvarjamo dobiček in podobno. Postopek takega poslovanja imenujemo obrestovanje.
Najpogosteje se srečamo s t.i. navadnim obrestovanjem in obrestnim obrestovanjem, ki ga lahko rešujemo kot matematični problem z uporabo aritmetičnega in geometrijskega zaporedja.
Navadno ali enostavno obrestovanje je obrestovanje, pri katerem se ves čas obrestuje le začetni kapital brez dodanih obresti. To pomeni, da znesek kapitala v vsakem obrestovalnem obdobju naraste za vedno enako denarno vrednost.
Dobljene obresti pri navadnem obrestovanju glavnice G, ki jo n let navadno obrestujemo s p % obrestno mero, zapišemo kot:
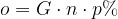
ali
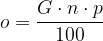
Pri navadnem obrestovanju začetni kapital vedno narašča linearno, zato ga imenujemo tudi linearno obrestovanje. To pomeni, da po 1, 2, ..., n letih in z upoštevanjem, da se v posameznem obrestovalnem obdobju glavnica G poveča za enako višino obresti, vrednosti glavnice znašajo:
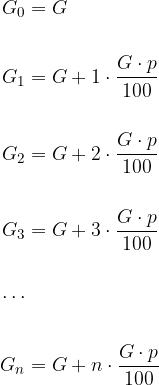
Po n letih višina kapitala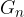 
pri linearnem obrestovanju znaša:
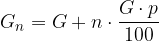
Postopek obrestovanja ponazorimo še na grafu za znesek G = 10 000 € in obrestno mero p = 5 %:
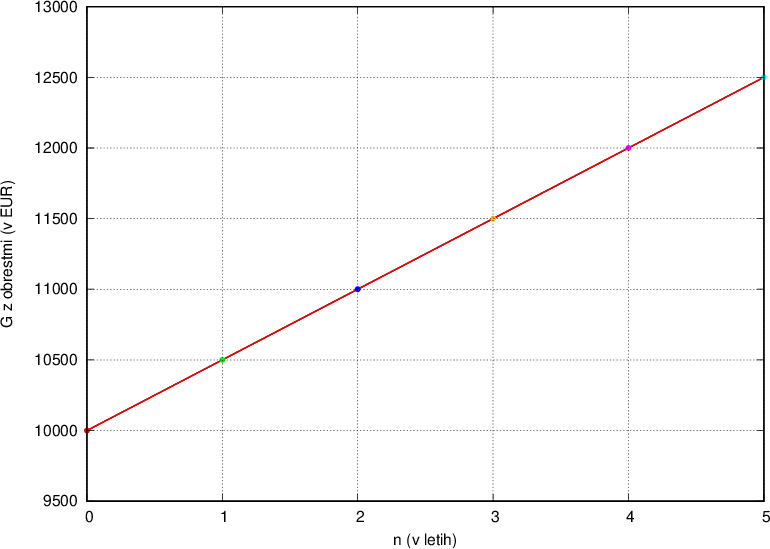
Očitno je obrestovanje res linearno (graf je premica), zaporedne vrednosti glavnice pa sestavljajo aritmetično zaporedje.
Opomba: Navadno obrestovanje se dandanes pri denarnem poslovanju uporablja zelo redko.
Obrestno obrestovanje je obrestovanje, pri katerem se poleg začetnega kapitala obrestujejo tudi obresti. To pomeni, da v vsakem obrestovalnem obdobju dobljene obresti prištejemo glavnici in v nadaljnjem obrestovalnem obdobju obrestujemo glavnico s prištetimi obrestmi iz predhodnega obdobja.
Obrestno obrestovanje prinaša večje obresti kot navadno obrestovanje, saj se namesto glavnice v bistvu obrestuje kapital, ki se povečuje z zaključkom vsakega obrestovalnega obdobja.
Izračunajmo obresti, če imamo glavnico G, ki jo n let obrestno obrestujemo s p % letno obrestno mero:
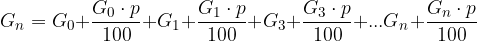
Upoštevamo:
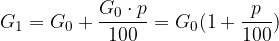
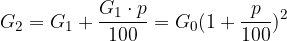
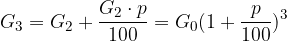
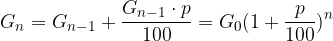
in dobimo:
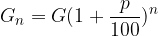
Opazimo, da je imajo vse vrednosti glavnice skupen količnik zaporedja oblike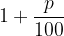 
, kar imenujemo letni obrestovalni faktor.
Letni obrestovalni faktor, kjer je p letna obrestna mera, označimo z oznako r:
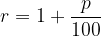
Zapišimo vrednost glavnice G še drugače.
Vemo, da velja:
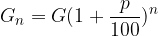
Uvedemo obrestovalni faktor in dobimo:
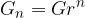
Pri obrestnem obrestovanju začetni kapital vedno narašča eksponentno. To pomeni, da po 1, 2, ..., n letih in z upoštevanjem, da se v posameznem obrestovalnem obdobju glavnica G poveča za pridobljene obresti v predhodnem obdobju, vrednosti glavnice znašajo:
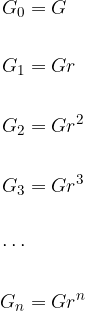
Postopek obrestovanja ponazorimo še na grafu za znesek G = 1000 € in obrestno mero p = 8 %:
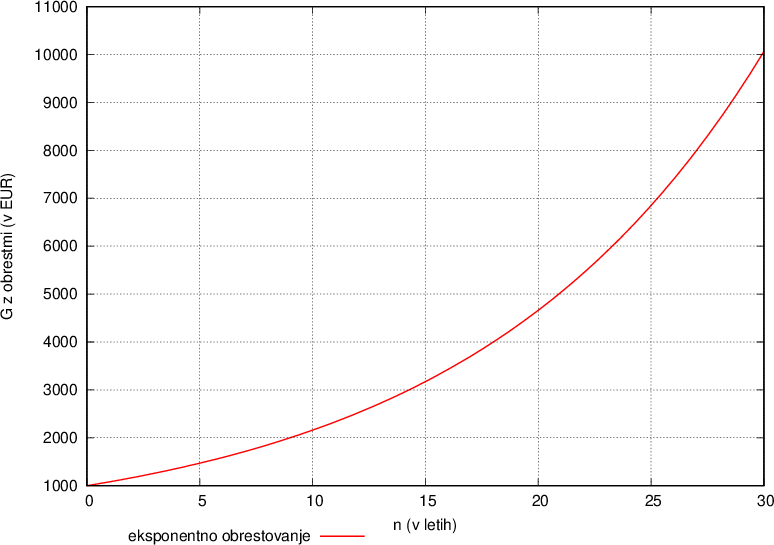
Očitno je obrestovanje res eksponentno, zaporedne vrednosti glavnice pa sestavljajo geometrijsko zaporedje s količnikom r. Glavnica narašča tem hitreje, večji kot je r oziroma čim večja je obrestna mera p.
Običajno v praksi pri obrestnem obrestovanju definiramo letno obrestno mero. Vendar lahko obrestno mero preračunavamo tudi na krajša časovna obdobja oz. pripisujemo obresti v polletnem obdobju ali pa na koncu vsakega meseca in celo dneva.
Pri polletni obrestni meri se glavnici pripišejo obresti po 6 mesecih obrestovanja, ki se nato, skupaj z glavnico, obrestujejo naprej, v naslednjih 6 mesecih.
Tako je polletna obrestna mera enaka:
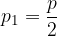
Pri mesečni obrestni meri pa se glavnici obresti pripisujejo mesečno, ki se nato skupaj z glavnico obrestujejo naprej, v naslednjem mesecu.
Mesečna obrestna mera je enaka:
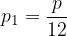
Ko imamo polletno/četrtletno/mesečno/dnevno obrestovalno obdobje in polletno/četrtletno/mesečno/dnevno obrestno mero, potem velja da:
Glavnica v m polletjih/četrtletjih/mesecih/dneh naraste na:
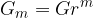
pri čemer je obrestovalni faktor:
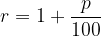
Kadar imamo obrestno mero za krajša kapitalizacijska obdobja, imamo pri izračunu obresti na voljo dve različni obrestni meri:
relativno oz. proporcionalno obrestno mero - za pogostejšo (na primer polletno, četrtletno, mesečno ali dnevno) kapitalizacijo se uporabljajo obrestne mere, ki so tolikokrat manjše od letne obrestne mere, kolikorkrat je kapitalizacijsko obdobje krajše od enega leta dni,
konformno oz. efektivno obrestno mero - za realizacijo ekonomskega načela, ki pravi, da moramo iz začetne glavnice s konformno obrestno mero pri pogostejši kapitalizaciji (mesečni) dobiti enako končno vrednost glavnice, kot pri celoletni kapitalizaciji in izhodiščni letni obrestni meri.
Pri uporabi relativne obrestne mere velja, da ob redukciji upoštevamo in prilagajamo obrestno mero na krajša kapitalizacijska obdobja (delimo s številom kapitalizacijskih obdobij).
Ko je kapitalizacija z letno obrestno mero p krajša od enega leta in imamo v enem letu m kapitalizacijskih obdobij potem je pri relativnem obrestovanju
obrestovalni faktor enak:
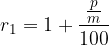
glavnica pa:
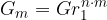
Uporaba relativne obrestne mere v bistvu pomeni uporabo navadnega obrestnega računa pri plačilu obveznosti prej kot v enem letu. Vendar, ker so ustrezne obresti lastniku kapitala na voljo prej kot v letu dni, je dejanska obrestna mera avtomatično večja od pogodbene letne obrestne mere.
Na običajnem primeru lahko to hitro opazimo, saj relativna obrestna mera pri pogostejši kapitalizaciji daje večje obresti - dobimo vedno večje končne vrednosti glavnice - kot relativna obrestna mera pri celoletni kapitalizaciji. Kar je v celoti korektno in logično, saj se obresti pripisujejo h glavnici večkrat v nekem kapitalizacijskem obdobju, vendar pa bi morale biti po osnovnem načelu obrestno obrestnega računa obresti pri pogostejši kapitalizaciji enake celoletni.
Zato banke uporabljajo konformno obrestno mero, ki zagotavlja, da dobimo iz začetne glavnice enako končno vrednost glavnice, ne glede na to, kako pogosto je bilo obrestovanje. Namreč, konformna obrestna mera prinese v enem letu enake obresti kot letna obrestna mera pri celoletni kapitalizaciji.
Uporaba konformne obrestne mere pomeni, da ob redukciji obrestno mero prilagodimo tako, da obrestovalni faktor korenimo s pripadajočo kapitalizacijo.
Pri konformnem obrestovanju z letno obrestno mero p, ki je krajša od enega leta, in z m število kapitalizacijskih obdobij v enem letu dobimo
obrestovalni faktor, ki je enak:
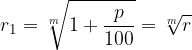
in glavnico:
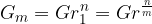
Konformno obrestovanje se v bankah pri novih poslih ne uporablja več, so pa nanj kot računsko metodo po zakonu vezani vsi izračuni t. i. efektivne obrestne mere kredita. To pomeni, da banke za kapitalizacijska obdobja, ki so krajša od enega leta, uporabljajo preračunan obrestovalni faktor pri konformnem obrestovanju.
Anticipativno obrestovanje - način obrestovanja, pri katerem posojilodajalec na začetku kapitalizacijskega obdobja obračuna obresti in jih odšteje od nominalne vrednosti glavnice.
Čas obrestovanja - časovno obdobje v katerem varčujemo oz. odplačujemo.
Dekurzivno obrestovanje - je pripis obresti, pri dekurzivni obrestni meri, na koncu kapitalizacijskega obdobja (npr. pri varčevanju).
Dolg - znesek sestavljen iz glavnice in obresti, ki ga dolgujemo oz. moramo odplačati.
Glavnica ali začetni kapital - denarni znesek, ki ga varčujemo, in se obrestuje.
Kapitalizacija - pripis obresti glavnici na koncu obrestovalne dobe.
Konformna ali efektivna obrestna mera - pomeni, da moramo iz začetne glavnice s konformno obrestno mero pri pogostejši kapitalizaciji (mesečni) dobiti enako končno vrednost glavnice, kot pri celoletni kapitalizaciji in izhodiščni letni obrestni meri.
Letna obrestna mera - nam pove, kolikšen odstotek od vplačanega ali prejetega zneska znašajo obresti na letni ravni. Izražamo jo v odstotokih.
Linearno obrestovanje - metoda za računanje obresti, pri katerem uporabljamo navadni obrestni račun.
Navadno obrestovanje - obrestovanje, pri katerem se obresti obračunavajo od prvotne glavnice.
Obresti - znesek, za katerega se poveča vrednost glavnice. Lahko tudi rečemo, da so obresti nadomestilo za uporabo določenega zneska denarja,
Obrestna mera - znesek, ki ga plačamo za izposojen denar oziroma prihodek, ki ga dobimo z varčevanjem. Izražamo jo v odstotkih.
Obrestovalna doba ali kapitalizacijsko obdobje - obdobje na koncu katerega se glavnici pripisujejo obresti. Običajna obrestovalna doba znaša mesec, četrtletje, polletje, eno leto.
Obrestno obrestovanje - obrestovanje, pri katerem se obresti prištevajo glavnici po vsakem kapitalizacijskem obdobju. Vsakič se obrestuje glavnica s prištetimi obrestmi.
Obrestovalni faktor - temelji na obrestni meri pri obrestnem obrestovanju.
Obrok ali anuiteta - je znesek, ki ga plačujemo posojilodajalcu v določenih časovnih obdobjih pri odplačevanju dolga.
Relativna obrestna mera - je obrestna mera, ki je tolikokrat manjša od letne obrestne mere, kolikokrat je kapitalizacijsko obdobje krajše od enega leta.
Vloga - znesek, ki ga vložimo v finančno ustanovo.
