Osebne zbirke


Primemo za obroč volana avtomobila in ga zavrtimo. Na volan smo delovali s silo F, ki deluje v smeri vrtenja volanskega obroča (glej sliko 1). Smer sile je torej tangenta na krožnico, ki jo predstavlja volanski obroč. Volan se zavrti okoli središča kroga, ki mu pravimo os vrtenja ali vrtišče. Razdalji med silo in osjo vrtenja pravimo ročica.
Produkt sile, s katero delujemo na volanski obroč in ročice, ki je enaka radiju r obroča, imenujemo navor:
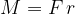
Zapisana enačba velja le, če sta sila in ročica pravokotni.
Navor bo tem večji, tem večja bo sila in / ali ročica.
Navoru damo pozitiven ali negativen predznak, odvisno od smeri vrtenja. Če se vrti v obratni smeri urinega kazalca je pozitiven, v smeri urinega kazalca pa negativno. To je v skladu s smerjo, v katero se vrti vijak, ki ga privijamo v npr. les:
Enota za navor je "Nm" (izgovorjava: njuten meter).
Navor je produkt sile in ročice:
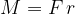
Sila in ročica sta pravokotna.
Navor je lahko pozitiven ali negativen. Predznak je odvisen od smeri vrtenja. Pozitivni navor je tisti navor, ki suka v obratni smeri urinega kazalca, negativni pa v smeri urinega kazalca.
V tem gradivu se bomo naučili:
kako računamo navor tudi, če sila in ročica nista pravokotni;
kako deluje navor na telo;
kako seštevamo in odštevamo navore;
spoznali bomo ravnovesje sil in navorov;
naučili se bomo, kaj je težišče telesa. Za preproste primere ga bomo tudi izračunali.
Navor je dejansko vektor. Ima svojo velikost in smer. Usmerjen je v smeri vektorskega produkta ročice in sile:
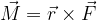
Navor je pravokoten na ravnino, na kateri ležita vektorja 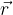 in
in 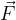 , kot kaže spodnja slika. Kako določimo smer vektorja navora? Ena od možnosti je, da z desno roko objamemo predmet (npr. izvijač) in ga zavrtimo v obratni smeri urinega kazalca. Iztegnjen palec kaže smer pozitivnega navora - slika levo. Predznak navora se spremeni, če zavrtimo v nasprotno smer - slika desno.
, kot kaže spodnja slika. Kako določimo smer vektorja navora? Ena od možnosti je, da z desno roko objamemo predmet (npr. izvijač) in ga zavrtimo v obratni smeri urinega kazalca. Iztegnjen palec kaže smer pozitivnega navora - slika levo. Predznak navora se spremeni, če zavrtimo v nasprotno smer - slika desno.
V tem gradivu bomo zaradi enostavnosti smatrali, da je navor skalar (število). Smer navora določimo:
navor je pozitiven, če skuša zavrteti v obratni smeri urinega kazalca;
navor je negativen, če vrti v smeri urinega kazalca;
V srednji šoli, kjer se računa navor kot skalarni produkt sile in ročice. Nekateri avtorji upoštevajo, da pozitivni navora suka v smeri urinega kazalca, negativni pa v nasprotno smer. Pri izračunu dobimo enak rezultat, le dosledno moramo upoštevati izbrano smer navora.
Zapišimo navor še enkrat brez vektorskega znaka:
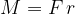
Navor je produkt sile in ročice. Sila in ročica morata biti pravokotna. V primeru, da to ni res, imamo na voljo dve možnosti:
izračunamo komponento sile, ki je pravokotna na ročico ali pa
izračunamo komponento komponento ročice, ki je pravokotna na silo.
Poglejmo podrobneje obe možnosti.
Izračunajmo navor, ko imamo dano silo in ročico, ki med seboj nista pravokotni. Vemo, da je navor največji, ko dana sila deluje pravokotno na ročico. Če sila ni pravokotna na ročico, moramo poiskati komponento sile, ki je pravokotna na ročico - glej sliko 3.
Označimo kot 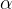 med smerjo sile F in pravokotnice na ročico. Silo F razstavimo na dve komponenti:
med smerjo sile F in pravokotnice na ročico. Silo F razstavimo na dve komponenti:
Prva komponenta je vzporedna z ročico
Na sliki 3 je označena s 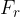 .
.
Izračunamo jo s pomočjo sinusa kota 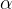 :
:
Ta komponenta ima enako smer kot ročica in zato ne povzroča navora.
Druga komponenta je pravokotna na ročico
Na sliki 3 je označena s 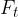 .
.
Izračunamo jo s pomočjo kosinusa kota 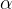 :
:
Ta komponenta kaže v smeri tangente kroga vrtenja, zato jo imenujemo tangencialna sila. Tangencialna sila povzroča navor.
Splošna enačba za navor se zapiše kot:
Navor povzroči komponenta sile, ki je pravokotna na ročico. Če z 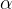 označimo kot med smerjo sile in pravokotnico na ročico, potem navor izračunamo z enačbo:
označimo kot med smerjo sile in pravokotnico na ročico, potem navor izračunamo z enačbo:
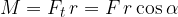
Tudi v tem primeru bomo računali navor, ko imamo dano silo in ročico, ki med seboj nista pravokotni. Silo F bomo premaknili vzdolž njene osi tako, da bo pravokotna na neko novo ročico 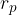 (glej sliko 4):
(glej sliko 4):
Med prejšnjo in novo ročico je ponovno kot 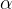 .
.
Izračunajmo navor:
Silo lahko premaknemo vzdolž njene osi tako, da bo pravokotna na neko novo ročico 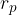 . Navor v tem primeru izračunamo z enačbo:
. Navor v tem primeru izračunamo z enačbo:
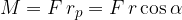
Na telo naj deluje več navorov. Vsoto ali rezultanto navorov, ki delujejo na telo dobimo tako, da jih seštejemo.
Vsota n navorov je:
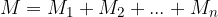
Pri seštevanju navorov moramo paziti na predznak navora. Ponovimo:
če povzroči navor vrtenje v obratni smeri urinega kazalca, je pozitiven.
če povzroči navor vrtenje v smeri urinega kazalca je negativen.
V gradivu Sila kot vektor smo se naučili, da je telo v ravnovesju, če je vsota sil, ki deluje na telo nič. V tem primeru telo miruje ali pa se giblje enakomerno in premočrtno.
Kaj pa, če je vsota sil enaka nič, vsota navorov pa različna od nič? V tem primeru povzroči navor vrtenje telesa. Telo se vrti enakomerno pospešeno. Ta primer bomo spoznali v gradivu Vrtilna količina.
V tem gradivu bomo se bomo omejili na primer, ko je vsota vseh sil in vsota vseh navorov enaka nič. Telo je takrat v mehanskem ravnovesju. To pomeni, da se ne giblje in ne vrti (ali pa, da se giblje enakomerno in premočrtno in enakomerno vrti).
Če se telo:
ne giblje in ne vrti ali
se giblje enakomerno in premočrtno oziroma se enakomerno vrti
je telo v mehanskem ravnovesju. Pogoj za mehansko ravnovesje je, da je vsota vseh sil, ki delujejo na telo in vsota vseh navorov nič:
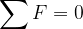
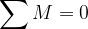
Polžasta vzmet je elastičen jeklen trak, navit v obliki polža. Uporablja se v nemirkah analognih ur, merilnih inštrumentih za merjenje električnih veličin, pa tudi za merjenja navora. Delovanje polžaste vzmeti prikazuje slika 8:
Opišimo dogajanje na sliki 8: zunanji konec polžaste vzmeti je pritrjen na podlago. Na sredini vzmeti je pritrjena ročica tako, da je vrtljiva okoli osi, ki je v središču vzmeti. Vzmet je na začetku v ravnovesju in na njej ni navora (slika 8, levo).
Nato začnemo delovati na vzmet s silo 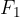 , ki je oddaljena za ročico
, ki je oddaljena za ročico  . Ustvarimo navor
. Ustvarimo navor 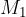 :
:
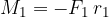
A danemu zasuku se upira navor polžaste vzmeti 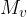 (slika 8, desno). Z merjenji ugotovimo, da je navor polžaste vzmeti sorazmeren s kotom zasuka
(slika 8, desno). Z merjenji ugotovimo, da je navor polžaste vzmeti sorazmeren s kotom zasuka 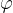 (kot je podan v radianih). Faktor sorazmernosti je konstanta vzmeti D.
(kot je podan v radianih). Faktor sorazmernosti je konstanta vzmeti D.
Zapišemo enačbo za navor polžaste vzmeti:
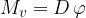
V ravnovesju bosta oba navora enaka:
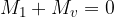
oziroma:
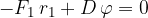
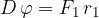
Če z zunanjim navorov zasukamo polžasto vzmet za kot 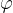 , deluje vzmet nazaj z nasprotnim, enako velikim navorom:
, deluje vzmet nazaj z nasprotnim, enako velikim navorom:
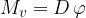
Enota za kot 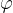 je radian.
je radian.
Ena od sil, ki povzroča navor, je sila teže telesa. Do zdaj smo obravnavali primere, ko:
je bilo telo majhno;
ročica pa - v primerjavi z dimenzijo telesa - velika.
Navor teže takega telesa z maso m in ročico r smo izračunali z enačbo:
Zdaj pa vzemimo telo z maso m, ki je veliko v primerjavi z ročico r. Navora ne moremo več enostavno izračunati po prejšnji enačbi, saj ima vsak delček tega telesa različno ročico in s tem prispeva k skupnemu navoru sile teže drugačno vrednost (glej sliko 9).
Takega problema se lotimo tako, da telo razdelimo na neskončno majhnih mas, vsaka z lastno težo. Da bomo lažje računali, vzemimo n majhnih mas, pri čemer je n veliko število. Izberemo si vrtišče telesa in računamo navore sil teže posameznih mas (slika 9, levo). Paziti moramo, da so sile teže in ročice pravokotne, zato prestavimo sile teže vzdolž njihovih osi tako, da so pravokotne na ročice (slika 9, desno).
Zaradi preglednosti slike narišemo telo dvodimenzionalno in se omejimo na štiri majhne mase.
Izračunajmo vsoto navorov v vrtišču T po sliki 9:
Uvedimo težišče: težišče je tista točka telesa, da če vanjo postavimo vrtišče, se bodo vsi navori sile teže danega telesa sešteli v nič.
Če je točka T na sliki 9 postavljena v težišče, se enačba poenostavi v:
Težišče telesa je tisto vrtišče, kjer se je vsota navorov teže enaka nič. Oziroma: vsota navorov teže vseh delnih mas, ki sestavljajo telo, je enaka nič, če je vrtišče postavljeno v težišče telesa.
Težišče si lahko predstavljamo tudi kot točko, kjer je (za potrebe računanja) združena vsa masa telesa.
Iskanje težišča si lahko olajšamo tako, da obesimo telo na tanko vrvico in počakamo, da se umiri. Smer vrvice je premica, okoli katere so vsi navori sile teže v ravnovesju ne glede, kje na premici vzamemo os vrtenja. Premica se imenuje težiščnica. Če bi želeli dobiti težišče, bi večkrat ponovili poskus in vsakokrat obesili telo na drugo mesto, kot kaže slika. V presečišču premic bi dobili težišče - slika 10.
Navor teže geometrijskega telesa računamo tako, da si celotno maso telesa mislimo zbrano v eni točki, ki je v težišču telesa. Tako telo imenujemo točkasto telo.
Poglejmo nekaj teles, za katera intuitivno vemo, kje imajo težišče:
Za kvader vemo, da ima težišče v središču - to je presečišču telesnih diagonal.
Krogla ima težišče v središču krogle.
Valj ima težišče na sredini geometrijske osi.
Poleg znanim predmetom pa lahko težišče določimo s poskusom z vrvico poljubnemu geometrijskemu telesu. Navor teže geometrijskega telesa izračunamo po enačbi:
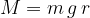
pri tem pa moramo v enačbi upoštevati, da je ročica r razdalja med vrtiščem in težiščem telesa.
Pri računanju navora poljubnega telesa moramo za ročico vzeti razdaljo med vrtiščem in težiščem telesa.
Na premici imamo n točkastih teles. Težišče sistema točkastih teles izračunamo po naslednjih korakih:
Najprej si izberemo vrtišče.
Nato izračunamo navore teže glede na izbrano os vrtenja in jih seštejmo:
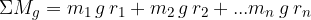
Navore tež vseh mas izenačimo z "nadomestnim" navorom. Ročica nadomestnega navora je ravno ročica do težišča, masa nadomestnega navora pa je celotna masa sistema:
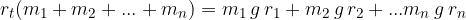
in izrazimo ročico med vrtiščem in težiščem:
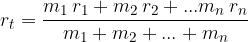
ali kratko:
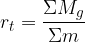
Razdalja težišča do izbranega vrtišča v primeru točkastih teles, razporejenih po premici, je:
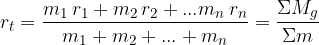
Tu so 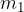 ,
, 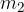 , ...,
, ..., 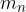 mase točkastih teles in
mase točkastih teles in  ,
, 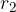 ,...,
,..., 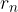 njihove oddaljenosti od izbranega vrtišča.
njihove oddaljenosti od izbranega vrtišča.