Osebne zbirke


Računanje nedoločenega integrala je obratna operacija od odvajanja - iz danega odvoda iščemo prvotno funkcijo. Nedoločeni integral funkcije f(x) označimo:
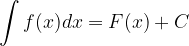
Funkcijo 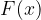 , ki jo dobimo z integriranjem, imenujemo primitivna funkcija. Ker je odvod konstante enak nič, prištejemo primitivni funkciji poljubno konstanto C - aditivno konstanto.
, ki jo dobimo z integriranjem, imenujemo primitivna funkcija. Ker je odvod konstante enak nič, prištejemo primitivni funkciji poljubno konstanto C - aditivno konstanto.
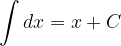
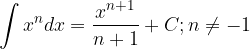
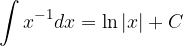
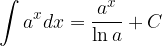
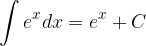
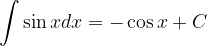
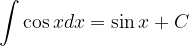
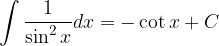
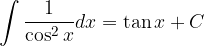
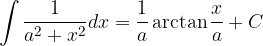
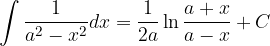
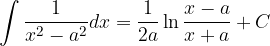
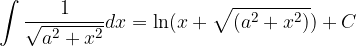
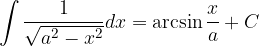
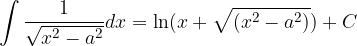
Poglejmo osnovna pravila integriranja.
Integral vsote oziroma razlike je enak vsoti oziroma razliki integralov.
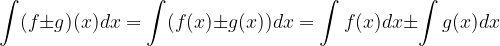
Konstanto pred funkcijo, ki jo integriramo, lahko zapišemo pred integralskim znakom.
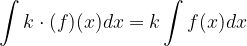
Imejmo integral naslednjega tipa:
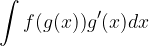
Integriranja se lotimo tako, da uvedemo novo spremenljivko:
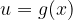
Odvod nove spremenljivke je:
V naš začetni integral vstavimo novo spremenljivko:
Integral v obliki 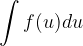 je velikokrat reševati enostavneje kot pa originalni zapis
je velikokrat reševati enostavneje kot pa originalni zapis 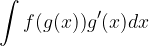 .
.
Pravilo največkrat uporabljamo pri integraciji produkta algebrske funkcije (npr. kvadratne, potenčne, polinomske, korenske,... funkcije) in transcendentne funkcije (npr. eksponentne, logaritemske, trigonometrične,... funkcije) ali pri produktu dveh transcendentnih funkcij.
Naj bosta 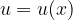 in
in 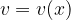 odvedljivi funkciji.
odvedljivi funkciji.
Odvajajmo njun produkt:
Z integriranjem po delih lahko v določenih situacijah pretvorimo prvoten integral v veliko bolj enostaven integral. Paziti pa moramo, da izberemo za 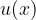 tisti del integrala, ki se pri odvajanju poenostavi.
tisti del integrala, ki se pri odvajanju poenostavi.
Za integriranje po delih uporabimo formulo:
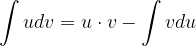
Če moramo integrirati racionalno funkcijo in integrala ne znamo izračunati na enega od zgoraj opisanih načinov, potem običajno poskušamo takšno funkcijo zapisati kot vsoto parcialnih ulomkov. Takšne ulomke pa lahko integriramo.