Osebne zbirke
Prijava z e-naslovom
Prijava brez gesla
Število a je ničla polinoma, ko je vrednost polinoma v tej točki enaka 0.
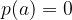
V tem primeru je polinom p(x), deljiv z linearnim polinomom (x-a).
Vrednost a je ničla polinoma
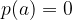
ko pri deljenju polinoma z
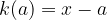
dobimo izraz oblike
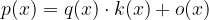
in je pri tem ostanek o(x) enak nič:
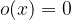
Polinom n-te stopnje ima kvečjemu toliko ničel kot je njegova stopnja.
Polinom n-te stopnje lahko ima tudi večkratne ničle.
Vsak poljuben polinom n-stopnje lahko zapišemo v obliki produkta linearnih polinomov. To je posledica osnovnega izreka algebre.
Osnovni izrek algebre pravi, da ima vsak nekonstanten polinom s kompleksnimi koeficienti vsaj eno kompleksno ničlo.
Pri polinomih z realnimi koeficienti kompleksne ničle nastopajo vedno v konjugiranih parih:
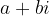
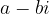
Posledica osnovnega izreka algebre je tudi trditev: vsak nekonstanten polinom z realnimi koeficienti lahko v obsegu realnih števil razcepimo na
produkt linearnih polinomov ALI
produkt linearnih polinomov in nerazcepni kvadratni polinom.
Linearni polinomi nam podajo ničle z realnimi koeficienti. Medtem ko sta rešitvi vsakega nerazcepnega kvadratnega polinoma dve konjugirani kompleksni ničli. Oglejmo si to na praktičnem primeru.
Vsak nekonstanten polinom lihe stopnje ima vsaj eno realno ničlo.
