Osebne zbirke


Pogosto se pri računanju določenih integralov srečujemo s funkcijami, katerih nedoločen integral ne moramo izraziti z elementarnimi funkcijami ali elementarne funkcije ne moremo določiti. V takih primerih se računanja integralov lotimo s pomočjo različnih numeričnih metod.
Trapezna metoda je ena izmed metod, s katerimi računamo približno vrednost integrala. Lik pod krivuljo na danem intervalu [a, b] razdelimo na n enakih delov in mu včrtamo oziroma očrtamo trapeze. To numerično metodo računanje za približne vrednosti integrala imenujemo trapezna metoda. Poglejmo si jo nekoliko podrobneje.
Integracijski interval 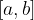 razdelimo na n enakih delov:
razdelimo na n enakih delov:
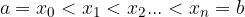
Tako smo dobili n manjših podintervalov:
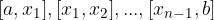
Širina vsakega delnega intervala je enaka:
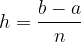
Nad intervale narišimo trapeze z osnovnicama 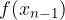 in
in 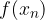 ter višino
ter višino 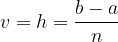
Približna vrednost določenega integrala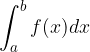 je enaka vsoti ploščin vseh trapezov:
je enaka vsoti ploščin vseh trapezov:
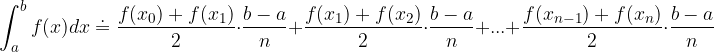
Uredimo:
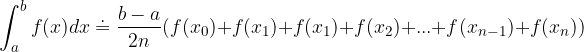
Trapezna formula za približen izračun določenega integrala: