Prijava z e-naslovom
Prijava brez gesla
Količine so lahko medsebojno odvisne.
Odnosov med odvisno in neodvisno količino je več vrst, eden izmed njih je obratno sorazmerje.
Če se pri:
dvakratnem, trikratnem ...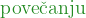 
prve količine
druga količina dvakrat, trikrat ... 
,
potem sta ti dve količini v obratnem sorazmerju.
Enako velja tudi v obratni smeri. Če se pri:
dvakratnem, trikratnem ... 
prve količine
druga količina dvakrat, trikrat ... 
,
potem sta ti dve količini v obratnem sorazmerju.
Če sta količini med seboj odvisni, nista nujno v obratnem sorazmerju.
Spomnimo se, kaj sta odvisna in neodvisna spremenljivka.
Količino, ki jo lahko poljubno izberemo ali spremenimo, imenujemo neodvisna spremenljivka. Običajno jo označimo z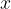 
.
Količina, ki se prilagaja drugi količini in je ne moremo poljubno izbirati, imenujemo odvisna spremenljivka. Običajno jo označimo z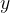 
.
V situaciji iz prejšnjega primera imamo dve spremenljivki:
Število otrok je neodvisna spremenljivka, saj je to lahko poljubno.
Količina čokolade, ki jo dobi vsak otrok, pa je odvisna spremenljivka, saj je odvisna od števila otrok.
Vpišimo v tabelo količino čokolade 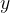za enega, dva, tri in štiri otroke :
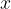Iz tabele razberemo, da je zmnožek števila otrok in količine čokolade na otroka vedno enak:
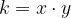
Zmnožek je vedno enak, ne glede na to, katero vrstico tabele gledamo. V matematiki število, ki se ne spreminja, imenujemo konstanta.
Kadar sta količini obratno sorazmerni, njun zmnožek imenujemo koeficient obratnega sorazmerja.
Koeficient k obratnega sorazmerja je zmnožek neodvisne in odvisne spremenljivke v obratnem sorazmerju:
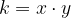
Koeficient obratnega sorazmerja je konstanta.
Če iz zapisa koeficienta obratnega sorazmerja
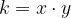
izrazimo odvisno spremenljivko 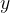, dobimo enačbo obratnega sorazmerja:
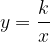
pri čemer:
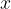predstavlja neodvisno spremenljivko,
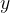predstavlja odvisno spremenljivko,
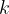pa je koeficient obratnega sorazmerja.
Enačba obratnega sorazmerja je:
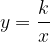
Kadar imamo dve količini, ki sta v obratnem sorazmerju, lahko namesto zamudnega merjenja obeh izmerimo zgolj eno, drugo pa izračunamo po enačbi ali s sklepanjem.
Obratno sorazmerje neodvisne količine 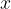in odvisne količine 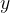v obliki enačbe zapišemo kot
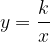
pri čemer je 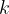koeficient obratnega sorazmerja.
Če želimo izračunati vrednost neznane količine 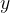, preprosto vstavimo 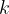in 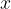v zgornjo enačbo in izračunamo njun količnik.
Če 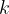ni podan, ga izračunamo iz znanih podatkov.
Če želimo izračunati vrednost neznane količine 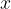, jo je potrebno najprej izraziti iz enačbe obratnega sorazmerja:
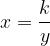
Vemo, da se pri obratnem sorazmerju z dvakratnim, trikratnim ... povečanjem prve količine druga količina dvakrat, trikrat ... zmanjša.
Enako velja tudi v obratni smeri. Z dvakratnim, trikratnim ... zmanjšanjem prve količine se druga količina dvakrat, trikrat ... poveča.
To z drugimi besedami pomeni, da se pri množenju prve količine z nekim številom vrednost druge količine istočasno deli z istim številom. Enako velja v obratni smeri. Če prvo količino delimo z nekim številom, se druga količina istočasno množi z istim številom.
Kadar eno količino pomnožimo z nekim številom, drugo pa istočasno delimo z istim številom, se zmnožek količin ne spremeni.
Še enkrat si oglejmo tabelo s količino čokolade na otroka iz zgornjega primera:
Naredimo nekaj izračunov za preizkus zgornje trditve:
Če podvojimo število otrok 2 v drugi vrstici tabele, dobimo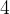 
otroke v četrti vrstici. Istočasno se količina čokolade razpolovi iz 
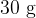na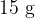 
. Zmnožek števila otrok in količine čokolade pa je tako v drugi kot v četrti vrstici enak 
.
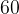Če število otrok 4 v četrti vrstici tabele delimo s 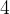, dobimo 
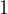otroka v prvi vrstici. Istočasno se količina čokolade množi s 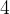, iz 
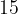na 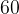. Zmnožek števila otrok in količine čokolade pa je tako v prvi kot v četrti vrstici enak .
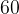Pri sklepanju ob zavedanju, da je zmnožek obeh vrednosti v isti vrstici tabele vedno enak:
izračunamo zmnožek količin v vrstici, kjer sta podani obe spremenljivki,
nato pa v vrstici, kjer ena spremenljivka manjka, zmnožek delimo z drugo spremenljivko.
Pri tej metodi računanja se izognemo tudi računanju koeficienta 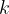obratnega sorazmerja.
Izračunajmo primera iz prejšnjega poglavja še s pomočjo sklepanja. S tem nam ne bo potrebno izračunati koeficienta 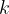obratnega sorazmerja.
