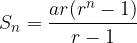Osebne zbirke


Vsakdo ima take ali drugačne želje, za katere pa velikokrat potrebuje denar (nakup stanovanja, plačilo šolnine, dodatek k penziji itd.). Vprašanje, s katerim se v takih situacijah vedno srečamo, je, kako priti do želenih denarnih sredstev?
Rešitev ponujajo banke, zavarovalnice, vzajemni skladi itd., kjer lahko izbiramo med možnostmi obročnega vplačevanja ali izplačevanja kot je npr. rentno varčevanje, življenjsko zavarovanje, vlaganje v vzajemne sklade in podobno.
Obročna vplačila ali izplačila so pomembna oblika dolžniško-upniškega razmerja in v vsakdanjem življenju zelo pogosta. Oglejmo si razlago izrazov, ki jih običajno srečamo v takih situacijah.
V vsakdanjem življenju se pogosto srečamo s t.i. obročnim vplačevanjem ali izplačevanjem enako visokih zneskov - obrokov - v enakih časovnih obdobjih.
Če dolgoročno varčujemo in redno vsak mesec na varčevalni račun polagamo enako visoke zneske, imenujemo to obročno vplačevanje.
Podobno lahko z rednimi izplačili, ponovno v enakih časovnih obdobjih, prejemamo del vrednosti nekega vloženega kapitala. Takrat govorimo o obročnem izplačevanju.
Če vlogo izčrpavamo v enakih obrokih, govorimo o renti.
Znesek, s katerim odplačujemo dolg v določenem časovnem obdobju, in je sestavljen iz dela glavnice dolga ter pripadajočih obresti, imenujemo anuiteta.
Mesečna anuiteta je mesečni obrok.
Če dolg odplačujemo v enakih obrokih in v enakih časovnih obdobjih, govorimo o amortizaciji dolga.
Izdelan načrt, kako bomo odplačali dolg v določenem časovnem obdobju, pa imenujemo amortizacijski načrt.
Pri obročnem vplačevanju vplačujemo obrok vsako leto, poljubno število let. Višino obroka v poljubni denarni valuti označimo z oznako a, število let vplačevanja pa označimo z oznako n.
Zapišemo potek obročnega vplačevanja:
Privzamemo, da vsakič vlagamo na koncu leta, zato se zadnja vloga ne obrestuje, predzadnja vloga se obrestuje eno leto, predpredzadnja vloga se obrestuje dve leti in tako naprej vse do prve vloge, ki se obrestuje 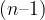 let.
let.
Povedano drugače, najprej plačamo obrok v znesku a, čez eno leto plačamo drugi obrok v višini a, čez dve leti tretji obrok v višini a in tako naprej do 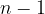 let, ko plačamo n-ti obrok v višini a.
let, ko plačamo n-ti obrok v višini a.
Vloge se obrestujejo z letnim pripisom obresti in z letno obrestno mero. Zapišimo dobljene naobrestene vloge:
Če dobljene vloge seštejemo, dobimo vsoto n enakih letnih obrokov v višini a, v času vplačila zadnjega obroka:
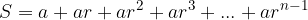
Očitno zaporedne vrednosti naobrestenih vlog sestavljajo geometrijsko zaporedje, vsota letnih obrokov pa je enaka končni geometrijski vrsti s količnikom r.
Obrazec za vsoto n enakih letnih obrokov v višini a, v času vplačila zadnjega obroka na koncu leta, se glasi:
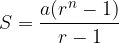
kjer je r enak ustreznemu obrestovalnemu faktorju pri obrestni meri p %:
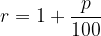
Vsoto označimo z oznako S.
Obročna vplačila lahko ponazorimo še na časovnem poltraku za znesek a in dobo n-tih let:
Z obročnim izplačevanjem označujemo črpanje vložene glavnice v obliki periodičnih zneskov. Taka obročna izplačila imenujemo rente in pravimo, da prejemamo rento.
Višino rente v poljubni denarni valuti označimo z oznako a, število let izplačevanja pa označimo z oznako n.
Velja:
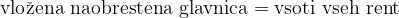
Višino obročnih vplačil ali izplačil lahko med seboj primerjamo, vendar le v istem časovnem terminu. Če imamo različne časovne termine ali različne valute vplačil oz. izplačil, podatkov med seboj ne moremo primerjati. Zato pri obračunu podatkov vedno upoštevamo načelo, ki pravi, da lahko vloženo glavnico in vsoto rent primerjamo le tako, da obe vrednosti preračunamo na isti časovni termin. Pravimo, da upoštevamo načelo ekvivalence glavnic.
Načelo ekvivalence glavnic pravi, da mora biti v istem časovnem terminu vsota ekvivalentnih vplačil enaka vsoti ekvivalentnih izplačil:
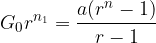
pri čemer z 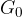 označimo vloženo glavnico, z
označimo vloženo glavnico, z 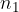 označimo čas od trenutka pologa do konca izplačevanja, z r označimo obrestovalni faktor, z n pa čas izplačevanja rent.
označimo čas od trenutka pologa do konca izplačevanja, z r označimo obrestovalni faktor, z n pa čas izplačevanja rent.
Glavnica je lahko privarčevana tudi s periodičnimi obroki, takrat pravimo, da velja 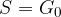 .
.
Za skupni časovni termin si lahko izberemo katerikoli časovni trenutek.
Najem posojila oz. kreditno poslovanje je sklenitev poslovnega odnosa, ki nastopa med banko kot posojilodajalcem in med najemnikom posojila kot posojilojemalcem. Sklenjeni posel je potrjen s podpisom posojilne (kreditne) pogodbe in obvezo, da bo posojilo odplačano v dogovorjenem obdobju.
Amortizacija dolga označuje odplačevanje takega najetega posojila oziroma dolga z obročnimi zneski v enakih časovnih obdobjih. Tak obročni znesek, ki je sestavljen iz dela glavnice dolga (razdolžnine) ter pripadajočih obresti, imenujemo anuiteta.
Višino anuitete v poljubni denarni valuti označimo z oznako a, število let odplačevanja dolga pa označimo z oznako n.
Tudi odplačevanje dolga se obračunava z uporabo načela ekvivalence glavnic. Velja:
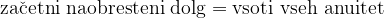
Začetni dolg in obresti obrestujemo od trenutka najema posojila do plačila zadnje anuitete. V tem istem obdobju se med seboj seštevajo tudi anuitete. Njihovo vsoto izračunamo z enakim postopkom kot izračunamo vsoto n enakih letnih obrokov.
Ker lahko znesek dolga in vsoto anuitet primerjamo samo v istem časovnem trenutku, moramo obe vrednosti preračunati na isti trenutek.
Načelo ekvivalence glavnic pri obračunu odplačevanju dolga pravi, da mora biti v istem časovnem terminu naobresteni dolg enak vsoti ekvivalentnih anuitet:
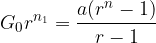
pri čemer z 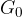 označimo začetni dolg, z
označimo začetni dolg, z 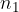 označimo čas od najema posojila do konca odplačevanja dolga, z r označimo obrestovalni faktor, z n pa čas odplačevanja dolga.
označimo čas od najema posojila do konca odplačevanja dolga, z r označimo obrestovalni faktor, z n pa čas odplačevanja dolga.
Za obračun odplačevanja dolga banka pripravi načrt odplačevanja dolga, ki ga imenujemo amortizacijski načrt.
Amortizacijski načrt je načrt odplačevanja dolga, ki v vsakem trenutku pokaže stanje glavnice posojila in plačanih obresti v posamezni dobi odplačevanja dolga.
Sestavljen je iz tabele s šestimi stolpci in n vrsticami:
Za sestavljanje amortizacijskega načrta upoštevamo naslednja pravila:
začetni dolg vnesemo v prvo vrstico tabele (stolpec 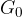 ),
),
obresti v n-ti vrstici izračunamo od dolga v isti vrstici (upoštevajoč p % obrestno mero in pripis obresti),
anuiteto v n-ti vrstici izračunamo od dolga v isti vrstici,
upoštevamo, da je anuiteta seštevek obresti in razdolžnin v pripadajoči n-ti vrstici,
ostanek dolga (OD) v n-ti vrstici izračunamo tako, da od dolga odštejemo razdolžnino,
ostanek dolga (OD) v n-ti vrstici zapišemo v naslednjo vrstico kot novi dolg,
ponovimo postopek dokler dolg ni poplačan (v stolpcu OD dobimo vrednost 0).
Vemo, da je posamezna anuiteta sestavljena iz dveh delov; en del je namenjen poplačilu obresti, drugi del pa je razdolžnina. Prav tako vemo, da pri kreditnem poslovanju v prvih letih odplačevanja v večji meri odplačujemo (samo) obresti, šele proti koncu obdobja začnemo pretežno odplačevati preostali del glavnice (razdolžnine). Zato velja, da se znesek obresti z leti manjša, znesek razdolžnine pa se povečuje, kar je očitno tudi iz amortizacijskega načrta (glej Slika 1).
Preverimo še naslednje pogoje:
zadnja razdolžnina mora biti enaka ostanku dolga v predhodni vrstici,
vsota razdolžnin je enaka začetnemu dolgu,
vsota vseh obresti in vseh razdolžnin mora biti enaka vsoti vseh anuitet.
Če znesek vložimo na začetku leta, se obrestuje eno leto manj kot pa če ga vložimo na koncu leta.
Če vplačilo vplačamo na začetku leta, se zadnja vloga obrestuje eno leto, predzadnja vloga se obrestuje dve leti, predpredzadnja vloga se obrestuje tri leta in tako naprej vse do zadnje vloge, ki se obrestuje n let.
Vsota n enakih letnih obrokov v višini a v času vplačila zadnjega obroka je tako enaka:
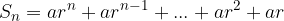
Obrazec za vsoto n enakih letnih obrokov v višini a, v času vplačila zadnjega obroka na začetku leta, pa se glasi: