Prijava z e-naslovom
Prijava brez gesla
Točke, premice in ravnine, ki se nahajajo v trirazsežnem prostoru, so lahko v različnih medsebojnih odnosih. Odnosi med njimi se nekoliko razlikujejo od tistih, ki smo jih spoznali v geometriji v ravnini.
K razširjenem naboru odnosov med točkami in premicami bomo dodali še odnose z ravnino.
Posamezne točke lahko zavzamejo poljubno mesto v prostoru. Za množice točk pa poznamo nekaj posebnih postavitev. Poglejmo si:
kolinearne točke,
nekolinearne točke,
komplanarne točke.
Točke, ki ležijo na isti premici, so kolinearne:
Dve točki sta vedno kolinearni.
Če točke ne ležijo na isti premici, so nekolinearne:
Nekolinearne točke
Skozi nekolinearne točke ne moremo potegniti ene premice.
Skozi poljubne tri nekolinearne točke lahko narišemo ravnino:
Tri nekolinearne točke natanko določajo ravnino.
Točke, ki ležijo na isti ravnini, so komplanarne točke.
Komplanarne točke
Poljubne tri točke so vedno komplanarne (tudi če so kolinearne). Čez vse tri točke lahko položimo vsaj eno ravnino.
Oglejmo si možne medsebojne lege točke in premice.
Točka lahko leži na premici:
Relacijo z matematičnimi simboli zapišemo kot
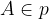
in preberemo: točka A leži na premici p.
Simbol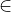 
sicer pomeni "je element množice". Vsaka premica je namreč množica točk. V zgornjem primeru je točka A ena od točk premice p.
Točka lahko leži izven premice:
Relacijo z matematičnimi simboli zapišemo kot
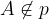
in preberemo: točka A ne leži na premici p.
Po dve premici lahko ležita v različnih medsebojnih legah. Oglejmo si jih.
V prostoru za vzporedni premici veljata dve pravili (pogoja):
premici nimata nobene skupne točke
Vzporedni premici nimata skupne točke
skozi premici lahko potegnemo eno ravnino
Vzporedni premici ležita na isti ravnini
Relacijo z matematičnimi simboli zapišemo kot
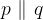
in preberemo: premica p je vzporedna s premico q.
Premici, ki se sekata, imata natanko eno skupno točko, ki jo imenujemo presečišče:
Relacijo z matematičnimi simboli zapišemo kot
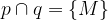
in preberemo: presek premic p in q je točka M.
Pravokotni premici predstavljata poseben primer presečišča premic. Sekata se namreč tako, da oklepata pravi kot (90° v stopinjah oziroma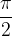 
v radianih):
Pravokotni premici
Relacijo z matematičnimi simboli zapišemo kot:
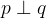
in preberemo: premica p je pravokotna na premico q.
Za mimobežni premici veljata dve pravili (pogoja):
premici nimata skupne točke in
skozi premici ne moremo potegniti ene ravnine.
Relacijo z matematičnimi simboli zapišemo kot
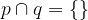
in preberemo: premici p in q nimata skupne točke.
Oglejmo si možne medsebojne lege točke in ravnine.
Relacijo z matematičnimi simboli zapišemo kot
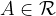
in preberemo: točka A leži na ravnini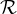 
Relacijo z matematičnimi simboli zapišemo kot
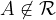
in preberemo: točka A ne leži na ravnini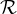
Sledijo možne medsebojne lege premice in ravnine.
Skozi dve različni točki, ki ležita na ravnini, lahko narišemo natanko eno premico. Taka premica leži na ravnini:
Relacijo z matematičnimi simboli zapišemo kot
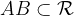
in preberemo: premica AB leži na ravnini 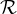. Premica in ravnina imata neskončno skupnih točk.
Simbol 
sicer pomeni "je podmnožica množice". Vsaka ravnina je namreč množica točk. Na zgornji sliki je premica podmnožica ravnine. Točke, ki ležijo na premici AB, ležijo hkrati tudi na ravnini .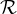
Premica seka (prebada) ravnino natanko v eni točki. To točko imenujemo prebodišče:
Relacijo z matematičnimi simboli zapišemo kot
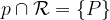
in preberemo: premica p seka ravnino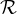 
v točki P.
Premica p in ravnina 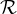imata torej eno samo skupno točko P.
Premica lahko seka ravnino pod pravim kotom.
Relacijo z matematičnimi simboli zapišemo kot
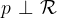
in preberemo: premica p je pravokotna na ravnino .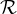
Premica p je pravokotna na ravnino 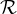le, če velja, da je pravokotna na vsaj na dve premici ravnine, q in r:
Pravokotnica na ravnino
Skozi vsako točko na ravnini lahko narišemo natanko eno pravokotnico na ravnino. Vse pravokotnice na ravnino so med seboj vzporedne. Predstavljajo snop premic.
Na ravnini vedno obstajata vsaj dve premici, na kateri je pravokotnica na ravnino pravokotna.
Če premica in ravnina nimata nobene skupne točke, sta vzporedni:
Relacijo z matematičnimi simboli zapišemo kot:
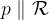
in preberemo: premica p je vzporedna z ravnino .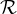
Velja, da premica p nima skupnih točk z ravnino :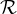
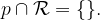
Dve ali več ravnin lahko zavzamejo različne medsebojne lege. Oglejmo si jih.
Ravnini sta vzporedni, če nimata skupnih točk:
Vzporedni ravnini
Relacijo z matematičnimi simboli zapišemo kot:
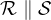
in preberemo: Ravnina 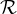je vzporedna z ravnino 
.
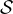Velja, da ravnini nimata skupnih točk:
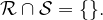
Presečišče dveh ravnin, ki nista vzporedni, je vedno premica:
Relacijo z matematičnimi simboli zapišemo kot
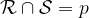
in preberemo: presečišče nevzporednih ravn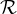in in 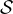je premica p.
Ravnini se lahko sekata pod pravim kotom. Na drugi ravnini vedno obstaja premica, ki je pravokotna na vsaj dve premici iz prve ravnine:
Pravokotni ravnini
Relacijo z matematičnimi simboli zapišemo kot:
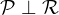
in preberemo: Ravnina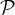 
je pravokotna na ravnino 
.
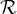Velja:
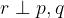
Presečišče treh ravnin je lahko:
Premica
Presečišče treh ravnin v premici
Točka
Presečišče treh ravnin v točki
