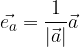Osebne zbirke


Če točki A v prostoru priredimo točko A', tako da velja:
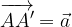
temu pravimo vzporedni premik (ali translacija) za vektor 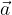 .
.
Velikost, smer in usmerjenost vzporednega premika ponazorimo z vektorjem, ki ga imenujemo vektor premika.
Naj bo 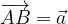 in
in 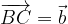 , kot kaže slika1.
, kot kaže slika1.
Pri seštevanju vektorjev upoštevamo Chaslesovo identiteto:
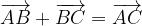
To grafično pomeni, da vektorja premaknemo tako, da leži končna točka prvega vektorja 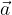 , v začetni točki drugega vektorja
, v začetni točki drugega vektorja 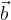 (točka B). Vektor, ki poteka od začetne točke prvega vektorja (točka A), do končne točke drugega vektorja (točka C), imenujemo vsota vektorjev
(točka B). Vektor, ki poteka od začetne točke prvega vektorja (točka A), do končne točke drugega vektorja (točka C), imenujemo vsota vektorjev 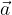 in
in 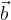 (glej slika2).
(glej slika2).
V primeru, ko imata vektorja skupno začetno točko (glej slika3), si pri seštevanju pomagamo s paralelogramskim pravilom, tako da skozi končni točki narišemo vzporednice k vektorjema. Vsota je diagonala dobljenega paralelograma.
Iz lastnosti seštevanja in odštevanja realnih števil izpeljemo naslednje lastnosti operacij z vektorji:
Asociativnostni zakon ali zakon o združevanju členov
Seštevanje vektorjev je asociativno:
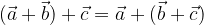
velja za poljubne vektorje 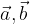 in
in 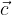 .
.
Komutativnostni zakon ali zakon o zamenjavi členov
Seštevanje vektorjev je komutativno:
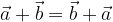
velja za poljubna vektorja 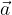 in
in 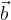 .
.
Enota za seštevanje ali ničelni vektor
Pri prištevanju vektorja 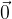 se vektor ne spremeni.
se vektor ne spremeni.
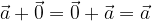
velja za vsak vektor 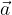 .
.
Inverz za seštevanje ali nasprotni vektor
Kadar vektorju prištejemo njegov nasprotni vektor, dobimo 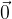 .
.
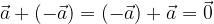
velja za vsak vektor 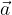 .
.
Naj bo 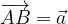 in
in 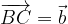 , kot kaže slika4.
, kot kaže slika4.
Odštevanje vektorjev definiramo kot prištevanje nasprotnega vektorja:
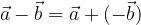
To grafično pomeni, da vektorju 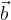 najprej spremenimo usmerjenost in nato ga premaknemo tako, da leži končna točka prvega vektorja
najprej spremenimo usmerjenost in nato ga premaknemo tako, da leži končna točka prvega vektorja 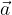 , v začetni točki drugega vektorja, vektorja
, v začetni točki drugega vektorja, vektorja 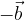 . Vektor, ki poteka od začetne točke prvega vektorja, do končne točke drugega vektorja, imenujemo vsota vektorjev
. Vektor, ki poteka od začetne točke prvega vektorja, do končne točke drugega vektorja, imenujemo vsota vektorjev 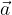 in
in 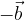 oz. razlika vektorjev
oz. razlika vektorjev 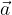 in
in 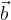 (glej Slika5).
(glej Slika5).
Vektorska enačba je enačba, v kateri kot neznanka nastopajo vektorji. rešujemo jih enako kot enačbe s številskimi spremenljivkami, torej neznan vektor prenesemo na eno stran in ga izrazimo.
Produkt vektorja 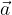 z realnim številom
z realnim številom 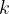 , različnim od nič, je vektor
, različnim od nič, je vektor 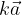 , ki ima:
, ki ima:
isto smer in usmerjenost kot vektor 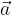 , če je
, če je 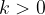
nasprotno usmerjenost kot vektor 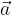 , če je
, če je 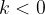
velikost 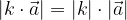
Iz lastnosti seštevanja in odštevanja realnih števil izpeljemo naslednje lastnosti operacij z vektorji:
Asociativnostni zakon v skalarnem faktorju ali zakon o združevanju členov
Za poljubni realni števili k, l in poljuben vektor 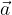 velja, da je množenje vektorjev s skalarjem asociativno:
velja, da je množenje vektorjev s skalarjem asociativno:
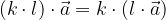
Distributivnostni zakon v vektorskem faktorju
Za poljubno realno število k in poljubna vektorja 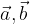 velja, da je množenje vektorjev s skalarjem distributivno v vektorskem faktorju:
velja, da je množenje vektorjev s skalarjem distributivno v vektorskem faktorju:
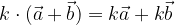
Distributivnostni zakon v skalarnem faktorju
Za poljubni realni števili k, l in poljuben vektor 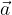 velja, da je množenje vektorjev s skalarjem distributivno v skalarnem faktorju:
velja, da je množenje vektorjev s skalarjem distributivno v skalarnem faktorju:
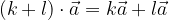
Enota za množenje
Za vsak vektor 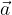 velja, da se pri množenju vektorja s številom 1, vektor ne spremeni:
velja, da se pri množenju vektorja s številom 1, vektor ne spremeni:
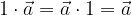
Enotski vektor
Enotski vektor vektorja 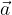 (
(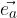 ) ima isto smer in usmerjenost kot vektor
) ima isto smer in usmerjenost kot vektor 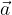 ter velikost 1:
ter velikost 1: