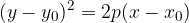Osebne zbirke


Parabola je množica vseh točk T(x,y) v ravnini, ki so enako oddaljene od premice vodnice (v) in od točke F (gorišče).
Geometrijsko definicijo parabole lahko zapišemo kot:
Razdaljo med goriščem parabole (F) in premico vodnico imenujemo parameter parabole p.
Značile elemente parabole najlažje preberemo s pomočjo skice:
elementi, ki so na skici tudi označeni, pa so:

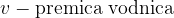
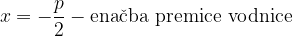
Parabola je krivulja drugega reda, zato tudi zanjo velja splošna enačba za krivulje drugega reda:
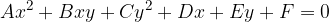
kjer sta 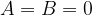 in se enačba preoblikuje v:
in se enačba preoblikuje v:
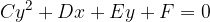
Pravzaprav, kot bomo kasneje ugotovili tudi prek enačb, je prabola kvadratna funkcija, ki je preslikana prek simetrale lihih kvadrantov. To lahko vidimo tudi tako, če v splošni enačbi krivulje drugega reda postavimo 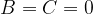 ; dobimo nič drugega kot kvadratno enačbo:
; dobimo nič drugega kot kvadratno enačbo:
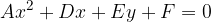
Parabola s temenom v koordinatnem izhodišču, je parabola, ki ima teme v točki A(0,0).
Poglejmo si skico te parabole:
Kot smo povedali v uvodu, je parabola množica točk, ki zadošča enačbi:
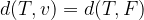
Iz grafa lahko zelo očitno razberemo obe razdalji in sicer za 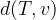 velja:
velja:
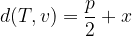
za 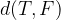 pa uporabimo navadno formulo za razdaljo med točkama:
pa uporabimo navadno formulo za razdaljo med točkama:
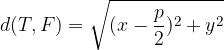
Iz povedanega lahko že izpeljemo enačbo parabole.
Enačba parabole s temenom A(0,0) je:
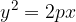
Če prvo parabolo prezrcalimo čez y os, dobimo drugo obliko parabole. Poglejmo si skico te parabole:
Pri zrcaljenju čez y os, se x v svojo negativno vrednost: 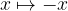 . Zapišimo enačbo preslikane parabole:
. Zapišimo enačbo preslikane parabole:
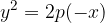
Odpravimo oklepaje in dobimo enačbo naše iskane parabole:
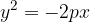
Enačba parabole, preslikane čez y os in s temenom A(0,0) je:
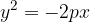
Če prvo parabolo zasukamo za kot 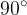 , dobimo novo obliko parabole. V tem primeru je parabola graf kvadratne funkcije.
, dobimo novo obliko parabole. V tem primeru je parabola graf kvadratne funkcije.
Izpeljimo enačbo parabole v tej legi s pomočjo uvodne definicije parabole, ki jo poznamo že iz uvoda:
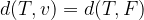
Iz grafa lahko zelo očitno razberemo obe razdalji in sicer za 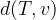 velja:
velja:
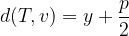
za 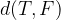 pa uporabimo navadno formulo za razdaljo med točkama:
pa uporabimo navadno formulo za razdaljo med točkama:
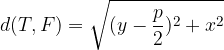
Iz povedanega lahko že izpeljemo enačbo parabole.
Opazimo, da sta se x in y - v primerjavi z enačbo prve oblike parabole - zamenjala, kar se zgodi, ko slikamo funkcijo čez simetralo lihih kvadrantov.
Enačba parabole, zasukane za 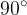 in s temenom A(0,0) je:
in s temenom A(0,0) je:
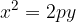
Če prvo parabolo zasukamo za kot  , dobimo novo obliko parabole. Tudi v tem primeru je parabola graf kvadratne funkcije.
, dobimo novo obliko parabole. Tudi v tem primeru je parabola graf kvadratne funkcije.
Opazimo, da je v tem primeru parabola enaka, kot če bi tretjo obliko parabole preslikali čez y os oziroma, če se 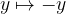 . Zapišemo enačbo preslikane parabole:
. Zapišemo enačbo preslikane parabole:
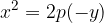
Odpravimo oklepaje in dobimo enačbo naše iskane parabole:
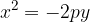
Enačba parabole, zasukane za  in s temenom A(0,0) je:
in s temenom A(0,0) je:
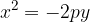
V primeru da parabolo premaknemo in sicer vsak 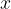 za
za 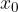 in vsak
in vsak 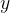 za
za 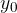 :
:
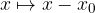
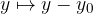
dobimo parabolo v premaknjeni legi.
Elementi, ki so na skici tudi označeni, so:

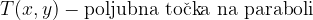
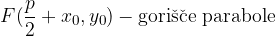
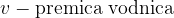
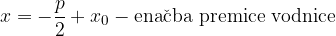
Enačba premaknjene parabole in s temenom v 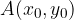 je:
je: