

Piramida je geometrijsko telo, katerega površje je sestavljeno iz več oglatih ravnih ploskev. Nasproti ene izmed ploskev vedno stoji vrh piramide. Ploskev pod vrhom imenujemo osnovna ploskev.
Piramide delimo na dve veliki skupini:
pokončne - vrh leži točno nad središčem osnovne ploskve,
poševne - vrh je zamaknjen od središča osnovne ploskve.
To je nekoliko ohlapen opis pokončnih in poševnih piramid. Lastnosti pokončnih piramid bomo podrobneje spoznali v nadaljevanju.
Kot smo videli, obstaja več vrst piramid, vsem pa lahko pripišemo nekaj skupnih lastnosti. Lastnosti piramid si bomo podrobno pogledali v nadaljevnaju.
Piramida je oglato geometrijsko telo, omejeno z:
eno osnovno ploskvijo,
plaščem.
Osnovna ploskev piramide je n-kotnik.
Plašč piramide je sestavljen iz n trikotnikov.
Za piramido so značilni naslednji elementi:
Osnovni robovi piramide so stranice osnovne ploskve (n-kotnika).
Stranski robovi so vsi ostali robovi piramide. To so daljice, ki povezujejo oglišča osnovne ploskve z vrhom piramide. Stranski robovi se torej stikajo v vrhu piramide.
Stranske ploskve piramide so trikotniki, ki sestavljajo plašč piramide.
Višina piramide je daljica, pravokotna na osnovno ploskev. Njena dolžina je enaka razdalji med osnovno ploskvijo in vrhom piramide.
Stranske višine so višine stranskih ploskev piramide.
V uvodu smo videli, da razlikujemo pokončne in poševne piramide. Poševne piramide so prezahtevne za okvir osnovne šole, zato se bomo v nadaljevanju osredotočili le na pokončne piramide.
V nadaljevanju obravnavamo le pokončne piramide.
Piramida je pokončna, če ima vse stranske robove enako dolge. To pa pomeni, da so vsi trikotniki, ki sestavljajo plašč piramide, enakokraki. Ni pa nujno, da so trikotniki v plašču tudi skladni. Kot bomo videli v nadaljevanju, velja skladnost stranskih ploskev le za pravilne in enakorobe piramide.
Za pokončno piramido veljajo naslednje posebnosti:
stranski robovi so skladni,
stranske ploskve so enakokraki trikotniki.
Omenjene posebnosti nam olajšajo računanje površine in prostornine piramide, ki ju bomo spoznali v nadaljevanju.
Površina piramide je njeno površje, ki ga sestavlja več mejnih ploskev. Izračunamo jo tako, da seštejemo ploščine vseh njenih mejnih ploskev. Mejne ploskve prizme so:
večkotnik in
Celotna površina piramide je razporejena po več ravninah. Da si površino lažje predstavljamo, mejne ploskve razgrnemo na eno ravnino.
Če mejne ploskve piramide razgrnemo na ravnino, dobimo mrežo piramide. Celotna mreža predstavlja sestavljen geometrijski lik.
Mejne ploskve telesa, razgrnjene na ravnino, imenujemo mreža geometrijskega telesa.
Računanje površine piramide si lahko predstavljamo kot računanje ploščine sestavljenega geometrijskega lika. Pri tem:
najprej izračunamo ploščine posameznih delov,
nato pa te ploščine seštejemo.
Osnovna ploskev piramide je n-kotnik. Zato za računanje njene ploščine ni enotne formule. Lahko pa zapišemo:
Ploščino osnovne ploskve piramide označimo z O.
Izračunamo jo enako, kot ploščino n-kotnika.
Kot smo že povedali, je plašč pokončne piramide sestavljen iz enakokrakih trikotnikov.
Ploščino plašča piramide označimo s pl.
Ploščina plašča piramide je seštevek ploščin vseh enakokrakih trikotnikov, ki ga sestavljajo.
Površino piramide izračunamo tako, da seštejemo ploščini:
osnovne ploskve,
plašča.
Splošna enačba za površino P piramide se glasi:
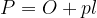
pri čemer je O ploščina osnovne ploskve, pl pa ploščina plašča piramide.
Prostornina piramide je velikost prostora, ki ga piramida zavzame.
Splošna enačba za izračun prostornine V piramide se glasi:
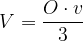
pri čemer je O ploščina osnovne ploskve, v pa višina piramide.
Poznamo več vrst piramid, ki jih ločimo po njihovih lastnostih. Lastnosti piramid pa so osnova za njihovo poimenovanje. Poglejmo, po katerih lastnostih jih ločujemo.
Piramido poimenujemo po n-kotniku, ki predstavlja osnovno ploskev.
Splošno lahko zapišemo:
Piramida, katere osnovna ploskev je n-kotnik, se imenuje n-strana piramida.
Osredotočimo se na robove piramide. Posebne primere predstavljajo piramide, ki imajo skladne:
osnovne robove,
vse robove v piramidi.
Poglejmo si obe skupini piramid podrobneje.
Piramido, ki ima skladne osnovne robove, poimenujemo pravilna piramida.
Osnovni robovi predstavljajo stranice osnovne ploskve. Mnogokotnik z enako dolgimi stranicami je pravilen, zato podobno zapišemo tudi za piramido.
Piramida je pravilna, če ima za osnovno ploskev pravilni n-kotnik.
Če ima piramida enako dolge vse robove (tako osnovne kot stranske), jo imenujemo enakoroba piramida.
Piramida je enakoroba, če ima vse robove enako dolge.
Za enakorobo piramido lahko zapišemo tudi naslednje:
Piramida, ki je enakoroba, je hkrati tudi pravilna.
Za posebne primere piramid veljajo poenostavljeni obrazci za izračun površine in prostornine. Izpeljemo jih iz osnovnih formul ob upoštevanju lastnosti posamezne piramide.
Podrobneje si bomo ogledali nekaj primerov:
tristranih,
štiristranih
pokončnih piramid.
Najprej si poglejmo tristrane piramide.
Pravilna tristrana piramida ima za osnovno ploskev enakostranični trikotnik:
Površina
Za lažji izračun površine narišimo mrežo piramide:
Ploščina osnovne ploskve pravilne tristrane piramide je enaka ploščini enakostraničnega trikotnika:
Enačba za ploščino osnovne ploskve pravilne tristrane piramide se glasi:
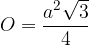
pri čemer je a dolžina osnovnega roba piramide.
Plašč piramide je sestavljen iz treh skladnih enakokrakih trikotnikov. Označimo ploščino trikotnika v plašču s 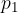 in izpeljimo enačbo za izračun plašča pravilne tristrane piramide. Izhajamo iz enačbe:
in izpeljimo enačbo za izračun plašča pravilne tristrane piramide. Izhajamo iz enačbe:
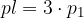
In izpeljemo obrazec:
Dobili smo enačbo za ploščino plašča pravilne tristrane piramide.
Enačba za ploščino plašča pravilne tristrane pokončne piramide se glasi:
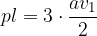
pri čemer je a dolžina osnovnega roba, 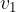 pa stranska višina piramide.
pa stranska višina piramide.
Izpeljimo še enačbo za površino pravilne tristrane piramide s splošno enačbo za površino piramide:
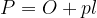
Zapišimo:
Dobili smo enačbo za površino pravilne tristrane piramide.
Enačba za površino pravilne tristrane piramide se glasi:
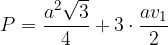
pri čemer je a dolžina osnovnega roba, 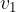 pa stranska višina piramide.
pa stranska višina piramide.
Za izračun stranskega roba  si lahko pomagamo s stransko višino
si lahko pomagamo s stransko višino 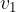 .
.
Stranska ploskev piramide je enakokraki trikotnik. Če ga razpolovimo pravokotno na osnovnico, dobimo dva pravokotna trikotnika:
Tako za levi kot za desni pravokotni trikotnik lahko zapišemo Pitagorov izrek:
Pri računanju stranske ploskve piramide uporabimo Pitagorov izrek na pravokotnem trikotniku:
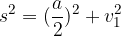
pri čemer je s dolžina stranskega roba, a dolžina osnovnega roba, 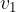 pa stranska višina piramide.
pa stranska višina piramide.
Pravilo velja splošno za vse pravilne pokončne piramide.
Prostornina
Izpeljimo še enačbo za prostornino pravilne tristrane piramide s splošno enačbo za prostornino piramide:
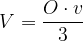
Zapišimo:
Dobili smo enačbo za prostornino pravilne tristrane piramide.
Enačba za izračun prostornine pravilne tristrane piramide se glasi:
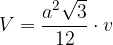
pri čemer je a dolžina osnovnega roba, v pa višina piramide.
Štiristrana pokončna piramida ima pravokotnik za osnovno ploskev:
Površina
Za lažji izračun površine narišimo mrežo piramide:
Ploščina osnovne ploskve štiristrane piramide je enaka ploščini pravokotnika:
Enačba za ploščino osnovne ploskve štiristrane piramide se glasi:
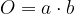
pri čemer sta a in b dolžina in širina osnovne ploskve piramide.
Napišimo še enačbo za izračun plašča. Stranske ploskve so enakokraki trikotniki, za katere velja:
vsi kraki so enako dolgi,
po dve nasprotni osnovnici sta skladni.
Trikotniki, iz katerih je sestavljen plašč piramide, so torej paroma skladni. Označimo ploščini prvega para s 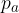 , drugega pa s
, drugega pa s 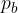 .
.
Za zapis ploščine plašča bomo izhajali iz enačbe:
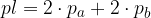
Izpeljimo enačbo za ploščino plašča:
Dobili smo enačbo za ploščino plašča štiristrane piramide.
Enačba za ploščino plašča štiristrane piramide se glasi:
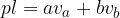
pri čemer sta a in b dolžina in širina osnovne ploskve, 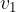 in
in 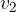 pa stranski višini piramide.
pa stranski višini piramide.
Vsaka stranska ploskev piramide je enakokraki trikotnik. Ti enakokraki trikotniki so lahko različnih velikosti. Piramida, ki ima za osnovno ploskev pravokotnik, ima v plašču:
dva enakokraka trikotnika z osnovnico a ter
dva enakokraka trikotnika z osnovnico b
Če razpolovimo enakokraki trikotnik z osnovnico a pravokotno na osnovnico, nastaneta dva pravokotna trikotnika, za katera lahko zapišemo Pitagorov izrek, s katerim izračunamo stranski rob piramide:
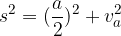
Na enak način kot zgoraj razpolovimo še enakokrak trikotnik z osnovnico b. Tudi v tem primeru nastaneta dva pravokotna trikotnika, za katera lahko zapišemo Pitagorov izrek:
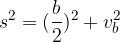
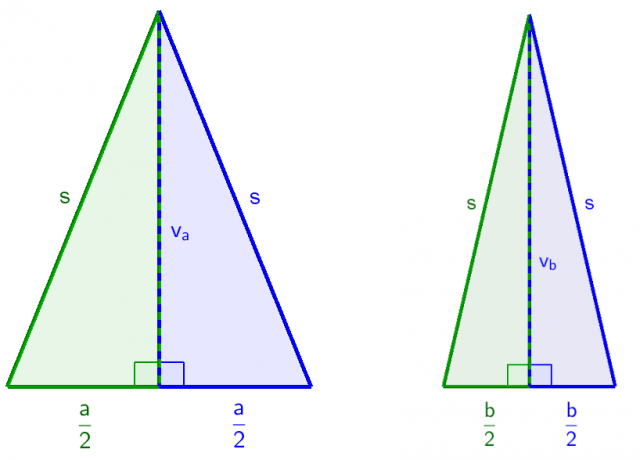
Levo - pravokotna trikotnika na stranski ploskvi pravilne tristrane piramide z osnovnico a,
desno - pravokotna trikotnika na stranski ploskvi pravilne tristrane piramide z osnovnico b
Zapišimo pravilo za uporabo Pitagorovega izreka pri računanju stranskega roba piramide:
Pri računanju stranskih robov  uporabimo Pitagorov izrek na pravokotnem trikotniku:
uporabimo Pitagorov izrek na pravokotnem trikotniku:
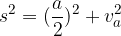
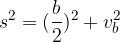
pri čemer sta a in b dolžini osnovnih robov, 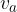 in
in 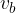 pa stranski višini piramide.
pa stranski višini piramide.
Izpeljimo še enačbo za površino pokončne štiristrane piramide s splošno enačbo za površino piramide:
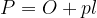
Zapišimo:
Dobili smo enačbo za površino pokončne štiristrane piramide.
Enačba za površino 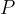 pokončne štiristrane piramide se glasi:
pokončne štiristrane piramide se glasi:
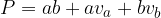
pri čemer sta a in b dolžina in širina osnovne ploskve, 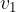 in
in 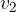 pa stranski višini piramide.
pa stranski višini piramide.
Prostornina
Izpeljimo še enačbo za prostornino pokončne štiristrane piramide s splošno enačbo za prostornino piramide:
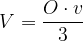
Zapišimo:
Dobili smo enačbo za prostornino pokončne štiristrane piramide.
Enačba za izračun prostornine 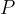 pokončne štiristrane piramide se glasi:
pokončne štiristrane piramide se glasi:
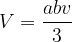
pri čemer sta a in b dolžina in širina osnovne ploskve, v pa višina piramide.
Obrazci za izračun stranksih višin in stranskega roba
Če štiristrano piramido prerežemo z ravnino, na kateri leži višina piramide ter dve izmed stranskih višin, dobimo enakokraki trikotnik. Možna sta dva preseka:
presek vzporedno s stranico a
presek vzporedno s stranico b
V obeh primerih enakokraki trikotnik razpolovimo pravokotno na osnovnico in dobimo dva pravokotna trikotnika, v katerih velja Pitagorov izrek:
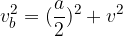
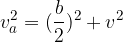
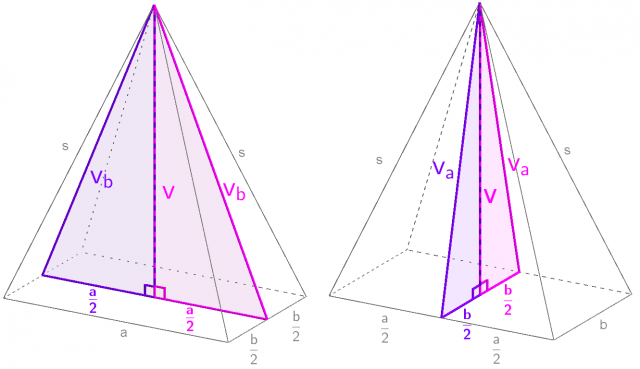
Levo: presek štiristrane piramide vzporedno z osnovnim robom a, desno: presek štiristrane piramide vzporedno z osnovnim robom b
Pitagorova izreka zapišimo še enkrat:
Višina, stranske višine in osnovni robovi so v štiristrani piramidi povezani preko Pitagorovih izrekov:
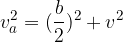
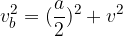
pri čemer sta 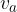 in
in 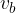 stranski višini, a in b dolžina in širina osnovne ploskve, v pa višina piramide.
stranski višini, a in b dolžina in širina osnovne ploskve, v pa višina piramide.
Štiristrano piramido lahko prerežemo tudi z ravnino, na kateri leži vrh diagonala osnovne ploskve 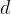 . Na tej ravnini leži višina piramide ter dva izmed stranskih robov. Tudi tu dobimo enakokraki trikotnik:
. Na tej ravnini leži višina piramide ter dva izmed stranskih robov. Tudi tu dobimo enakokraki trikotnik:
Enakokraki trikotnik zopet razpolovimo pravokotno na osnovnico. Dobimo dva pravokotna trikotnika, v katerih velja Pitagorov izrek:
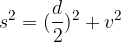
Zapišimo:
Višina, stranski robovi in diagonala osnovne ploskve so v štiristrani piramidi povezani preko Pitagorovega izreka:
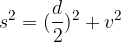
pri čemer je s stranski rob, d diagonala osnovne ploskve, v pa višina piramide.
Pravilna štiristrana pokončna piramida ima za osnovno ploskev kvadrat:
Površina
Za lažji izračun površine narišimo mrežo piramide:
Ploščina osnovne ploskve pravilne štiristrane piramide je enaka ploščini kvadrata.
Enačba za ploščino osnovne ploskve pravilne štiristrane pokončne piramide se glasi:
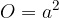
pri čemer je a dolžina osnovnega roba piramide.
Plašč piramide je sestavljen iz štirih skladnih enakokrakih trikotnikov. Označimo ploščine trikotnikov v plašču s 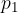 in izpeljimo enačbo za ploščino plašča pravilne štiristrane piramide. Pri izpeljavi izhajamo iz enačbe:
in izpeljimo enačbo za ploščino plašča pravilne štiristrane piramide. Pri izpeljavi izhajamo iz enačbe:
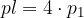
Izpeljimo enačbo za ploščino plašča:
Dobili smo enačbo za ploščino plašča pravilne štiristrane piramide.
Enačba za ploščino plašča 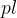 pravilne pokončne štiristrane piramide se glasi:
pravilne pokončne štiristrane piramide se glasi:
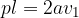
pri čemer je a dolžina osnovnega roba, 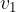 pa stranska višina piramide.
pa stranska višina piramide.
Stranska ploskev piramide je enakokraki trikotnik. Če ga razpolovimo pravokotno na osnovnico, dobimo dva pravokotna trikotnika:
Tako za levi kot za desni pravokotni trikotnik lahko zapišemo Pitagorov izrek:
Pri računanju stranskega roba  piramide uporabimo Pitagorov izrek na pravokotnem trikotniku:
piramide uporabimo Pitagorov izrek na pravokotnem trikotniku:
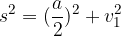
pri čemer je a dolžina osnovnega roba, 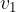 pa stranska višina piramide.
pa stranska višina piramide.
Izpeljimo še enačbo za površino pravilne štiristrane piramide s splošno enačbo za površino piramide:
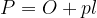
Zapišimo:
Dobili smo enačbo za površino pravilne štiristrane piramide.
Enačba za površino 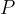 pravilne štiristrane pokončne piramide se glasi:
pravilne štiristrane pokončne piramide se glasi:
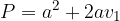
pri čemer je a dolžina osnovnega roba, 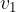 pa stranska višina piramide.
pa stranska višina piramide.
Prostornina
Izpeljimo še enačbo za prostornino pravilne pokončne štiristrane piramide s splošno enačbo za prostornino piramide:
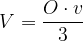
Zapišimo:
Dobili smo enačbo za prostornino pravilne pokončne štiristrane piramide.
Enačba za izračun prostornine 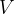 pravilne tristrane pokončne piramide se glasi:
pravilne tristrane pokončne piramide se glasi:
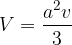
pri čemer je a dolžina osnovnega roba, v pa višina piramide.
Obrazca za stransko višino in stranski rob
Pravilno štiristrano piramido lahko skozi vrh razrežemo še:
po nasprotnih stranskih višinah 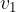 ,
,
po diagonali 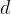 osnovne ploskve.
osnovne ploskve.
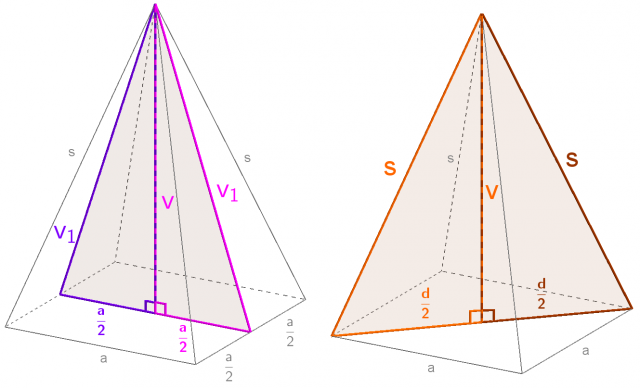
Levo: presek pravilne štiristrane piramide vzporedno z osnovnim robom a, desno: presek pravilne štiristrane piramide vzporedno z diagonalo osnovne ploskve d
Pri obeh razrezih dobimo enakokraki trikotnik. Ta enakokraki trikotnik pa razpolovimo na dva pravokotna trikotnika, na katerih lahko uporabimo Pitagorov izrek. S tem dobimo dva obrazca, ki nam pomagata pri računanju v nalogah:
Višina, stranske višine in osnovni robovi so v pravilni štiristrani piramidi povezani preko Pitagorovega izreka:
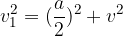
pri čemer je 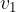 stranska višina, a osnovni rob, v pa višina piramide.
stranska višina, a osnovni rob, v pa višina piramide.
Višina, stranski robovi in diagonala osnovne ploskve so v štiristrani piramidi povezani preko Pitagorovega izreka:
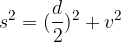
pri čemer je s stranski rob, d diagonala osnovne ploskve, v pa višina piramide.