Prijava z e-naslovom
Prijava brez gesla
O podobnosti med dvema predmetoma govorimo takrat, ko smo prepričani, da je en lik le povečan ali pomanjšan glede na drugega, sicer pa imata enako obliko in poteze.
O skladnosti pa govorimo takrat, ko se podobna lika ujemata tudi v velikosti, torej sta povsem enaka.
Na podlagi zgornjega primera lahko poenostavljeno rečemo:
Predmeta, ki imata enako obliko, sta si podobna.
Predmeta, ki imata enako obliko in enako velikost, sta skladna.
Če sta predmeta skladna, lahko katerega koli izmed njiju z vzporednimi premiki in zasuki "prestavimo" na drugega tako, da se natanko prekrivata.
Podobnost in skladnost lahko opazujemo tudi pri geometrijskih likih.
Pri ugotavljanju podobnosti likov smo pozorni na njihove lastnosti, predvsem na velikosti notranjih kotov in stranic.
Zgornji primer prikazuje lastnost podobnih likov:
Podobni liki:
se ujemajo v vseh notranjih kotih in
imajo enaka razmerja vseh parov istoležnih stranic.
Istoležne stranice v podobnih likih ležijo na krakih skladnih kotov.
Razmerje parov istoležnih stranic nam pove, kolikokrat so mere prvega lika večje oziroma manjše od drugega.
To razmerje imenujemo koeficient podobnosti in ga označimo z malo tiskano črko k.
Koeficient podobnosti predstavlja razmerje med istoležnimi dolžinami v podobnih geometrijskih likih:
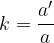
Pri tem a' in a predstavljata istoležni:
stranici
višini
diagonali itd.
Če je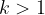 
, je kopija večja od originala, če je 
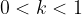, je kopija manjša od originala. Če je 
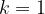, gre pa za skladna lika.
Če enačbo obrnemo, lahko na podlagi koeficienta podobnosti in znanih dolžin izračunamo neznane dolžine.
S pomočjo koeficienta podobnosti lahko ugotovimo, ali sta dva lika podobna ali ne:
če se koeficienti podobnosti za vse tri pare istoležnih stranic ujemajo, sta lika podobna,
če se vsaj en koeficient podobnosti razlikuje od preostalih, lika nista podobna.
Koeficient podobnosti lahko uporabimo tudi pri računanju z obsegom in ploščino podobnih likov.
Koeficient podobnosti predstavlja tudi razmerje med obsegoma podobnih geometrijskih likov:
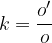
Kvadrat koeficienta podobnosti pa predstavlja tudi razmerje med ploščinama podobnih geometrijskih likov:
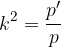
Dva lika sta skladna samo takrat, ko se ujemata v prav vseh lastnostih.
Zgornji primer prikazuje lastnost skladnih likov:
Skladni liki se natanko prekrivajo. Koeficient podobnosti k je enak 1.
