Osebne zbirke


Z besedo podobnost v vsakdanjem življenju opisujemo odnos med ljudmi ali predmeti, ki se med seboj ujemajo po neki bistveni lastnosti. Če imata na primer oče in sin ujemajoče se obrazne poteze, rečemo, da sta si podobna.
V matematiki je podobnost lastnost množic z enako obliko. Pri tem pa podobnost ločimo od skladnosti, ki je lastnost lastnost množic z enako obliko in velikostjo.
V geometriji v ravnini se bomo osredotočili na podobnost in skladnost geometrijskih likov, ki so sestavljeni iz množic točk. Pri razlagi snovi bomo privzeli, da bralec pozna pojme razmerje, sorazmerje in sestavljeno sorazmerje, ki so razloženi v gradivu Razmerje.
Ker so geometrijski liki sestavljeni iz množic točk, tudi zanje velja enako kot za množice:
Podobni geometrijski liki imajo enako obliko.
Skladni geometrijski liki imajo enako obliko in velikost.
Relacijo med podobnimi geometrijskimi liki določa koeficient podobnosti. Definiran je na naslednji način:
Koeficient podobnosti predstavlja razmerje med istoležnimi dolžinami v podobnih geometrijskih likih:
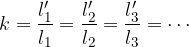
kjer so 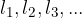 dolžine v prvem,
dolžine v prvem, 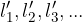 pa v drugem liku.
pa v drugem liku.
Ko govorimo o dolžinah v geometrijskih likih, mislimo na dolžine:
stranic,
višin,
diagonal,
težiščnic itd.
Koeficient podobnosti označuje tudi razmerje med obsegi podobnih n-kotnikov.
Ploščine podobnih n-kotnikov pa so v naslednjem razmerju:
Razmerje med ploščinama podobnih n-kotnikov je enako kvadratu koeficienta podobnosti:
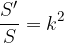
Podobna trikotnika sta enaka po obliki, po velikosti pa se razlikujeta:
Podobnost trikotnikov ABC in A'B'C' zapišemo kot:
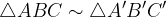
Definicija za podobnost trikotnikov se glasi:
Trikotnika sta podobna, če imata
enaka razmerja vseh stranic in
skladne vse notranje kote
Ker je vseh šest parametrov težko preverjati, si pomagamo z izreki o podobnosti trikotnikov:
Dva trikotnika sta si podobna, če se ujemata:
v dveh kotih
v dveh razmerjih enakoležnih stranic
v razmerju dveh stranic in vmesnem kotu ali
v razmerju dveh stranic in kotu, ki leži večji stranici nasproti
Izreki v nadaljevanju izhajajo iz podobnosti trikotnikov in se nanašajo na splošni oziroma pravokotni trikotnik:
Talesov izrek o sorazmerjih se glasi:
Če šop premic sekamo s snopom premic, je razmerje enakoležnih odsekov na katerem koli paru premic šopa vedno enako.
Če zgornji izrek poenostavimo do te mere, da tako šop kot snop predstavljata le po 2 premici, lahko zapišemo:
Premica, vzporedna poljubni stranici trikotnika, razdeli preostali stranici v enakem razmerju.
Izrek, ki povezuje simetralo kota in nasprotno stranico, se glasi:
Simetrala kota razdeli nasprotno stranico v razmerju stranic, ki ta kot oklepata:
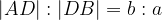
Pitagorov izrek se glasi:
Vsota kvadratov katet v pravokotnem trikotniku je enaka kvadratu hipotenuze:
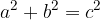
Pri tem sta kateti krajši stranici (a, b), ki tvorita pravi kot, hipotenuza (c) pa je najdaljša stranica in leži nasproti pravega kota:
Z razdelitvijo pravokotnega trikotnika z višino na hipotenuzo, dobimo dva nova pravokotna trikotnika, ki sta podobna prvotnemu trikotniku:
Na podlagi zgornje slike lahko zapišemo še tri izreke:
Višinski izrek se glasi:
Kvadrat višine na hipotenuzo c je enak zmnožku pravokotnih projekciji katet a in b na hipotenuzo:
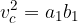
Na podoben način definiramo tudi Evklidova izreka:
Kvadrat katete je enak zmnožku hipotenuze in pravokotne projekcije katete na hipotenuzo:
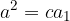
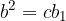
Skladna trikotnika sta enaka tako po obliki kot po velikosti:
Skladnost trikotnikov ABC in A'B'C' zapišemo kot:
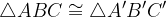
Definicija za skladnost trikotnikov se glasi:
Trikotnika sta skladna, če imata skladne
vse stranice in
vse notranje kote.
Ker je vseh šest parametrov težko preverjati, si pomagamo z izreki o skladnosti trikotnikov.
Dva trikotnika sta skladna, če se ujemata:
v dolžinah vseh treh stranic (načelo "stranica-stranica-stranica" oz. SSS)
v dolžinah dveh stranic in v kotu med njima (načelo "stranica-kot-stranica" oz. SKS)
v dveh kotih in v dolžini poljubne stranice (načelo "kot-stranica-kot" oz. KSK)
v dolžinah dveh stranic in v kotu, ki leži nasproti daljši od teh dveh stranic (načelo "večja stranica-manjša stranica-kot" oz. SSK)