Osebne zbirke


Popolna ali matematična indukcija je metoda, s katero preverjamo veljavnost neke predpostavke za vsa naravna števila. Kot orodje za dokazovanje je uporabna na mnogih področjih matematike.
Popolno indukcijo uporabljamo za dokazovanje veljavnosti nekega obrazca, trditve, enačbe, izjave, lastnosti ... v množici naravnih števil. Dokazovanje s popolno indukcijo temelji na dveh korakih:
najprej postavimo trditev in jo dokažemo za prvo naravno število, število 1. Povsem pričakovano je, da če trditev drži za celotno množico naravnih števil 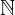 , potem zagotovo drži tudi za naravno število 1. Če trditev ne velja, potem je trditev napačna. Če pa trditev velja, nadaljujemo na drugi korak.
, potem zagotovo drži tudi za naravno število 1. Če trditev ne velja, potem je trditev napačna. Če pa trditev velja, nadaljujemo na drugi korak.
z drugim korakom želimo dokazati, da dana trditev velja, poleg za naravno število 1, še za vse ostale primere. To storimo tako, da:
najprej predpostavimo, da trditev velja za naravno število n
nato pa s predpostavko, da velja za n, dokažemo, da velja tudi za n + 1
Če ob predpostavki, da trditev velja za naravno število n, dokažemo, da velja tudi za n + 1, smo trditev - s pomočjo popolne indukcije - dokazali. Dokazali pa zato ker:
naj bo naš n = 1. Če trdite velja za n = 1, potem velja (dokazali v drugem koraku dokazovanja z indukcijo) tudi za n + 1 = 2. Ker pa smo v prvem koraku dokazovanja z indukcijo pokazali, da trditev za n = 1 velja, iz tega sledi, da trditev velja tudi za n = 2.
ker smo ravnokar ugotovili, da trditev velja za n = 2, iz drugega koraka indukcije sledi, da če trditev drži za n = 2, drži tudi za n + 1 = 3
in če trditev velja za n = 3, velja tudi za n + 1 = 4... in tak sklep lahko ponavljamo v neskončnost, za vsako naravno število.
Popolna indukcija:
v prvem koraku preverimo, ali dana trditev oziroma lastnost velja za prvo naravno število, torej če velja za 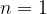 ;
;
v drugem koraku:
postavimo indukcijsko predpostavko:
" če trditev velja za neko naravno število 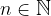 , potem velja tudi za njegovega naslednika
, potem velja tudi za njegovega naslednika 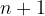 "
"
in indukcijsko predpostavko (ali indukcijski korak) dokažemo.
Z veljavnostjo obeh korakov je trditev dokazana za vsa naravna števila.
Včasih določena trditev ne velja za vsa naravna števila, temveč le za vsa naravna števila od neke vrednosti naprej. Tak primer je npr. obrazec za število diagonal v pravilnem n-kotniku:
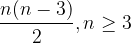
Za reševanje takih nalog postopek dokazovanja s popolno indukcijo smiselno spremenimo. Upoštevamo, da v prvem koraku ne dokazujemo trditve za prvo naravno število, temveč za prvo število, ko je naša trditev veljavna (se pravi, za 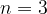 ). Drugi korak ostane nespremenjen.
). Drugi korak ostane nespremenjen.
Imamo zaporedje 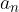 . Želimo izračunati vsoto prvih n členov zaporedja pa nismo prepričani, če je dan obrazec
. Želimo izračunati vsoto prvih n členov zaporedja pa nismo prepričani, če je dan obrazec 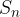 pravilen. S pomočjo popolne indukcije lahko pravilnost formule
pravilen. S pomočjo popolne indukcije lahko pravilnost formule 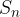 preverimo v dveh korakih:
preverimo v dveh korakih:
preverimo, če velja: 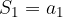
nato preverimo, če velja: 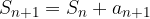
Z veljavnostjo obeh korakov dokažemo, da obrazec 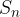 velja za vsak
velja za vsak 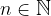 .
.