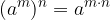Osebne zbirke


Potenca 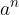 , kjer je
, kjer je 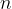 naravno število, je krajši zapis za produkt
naravno število, je krajši zapis za produkt 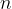 -faktorjev števila
-faktorjev števila 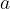 . Številu
. Številu 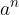 rečemo tudi
rečemo tudi 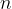 -ta potenca števila
-ta potenca števila 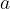 . Število
. Število 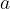 imenujemo osnova, število
imenujemo osnova, število 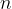 pa stopnja potence ali eksponent.
pa stopnja potence ali eksponent.
Potenca 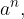 pri kateri je
pri kateri je 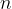 naravno število, je krajši zapis za produkt
naravno število, je krajši zapis za produkt 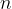 faktorjev števila
faktorjev števila 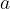 .
.
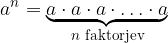
Vrednost potence 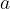
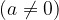 z negativnim celim eksponentom je:
z negativnim celim eksponentom je:
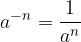
Za 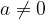 in
in 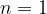 je
je
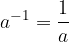
kar je obratna vrednost števila a.
Vrednost potence s poljubno neničelno osnovo in eksponentom 0 je 1:
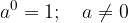
Povzetek pravil za računanje s potencami (pravila so v nadaljevanju podrobneje razložena) so povzeta v naslednji tabeli:
Pravilo za množenje potenc z enako osnovo ugotovimo tako, da obe potenci najprej zapišemo kot produkt enakih faktorjev.
Potence z enakimi osnovami množimo tako, da osnovo prepišemo, potenčne eksponente pa seštejemo:
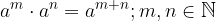
Pri deljenju potenc z enakimi osnovami ravnamo podobno kot pri množenju.
Potence z enakimi osnovami delimo tako, da osnovo prepišemo, potenčne eksponente pa odštejemo:
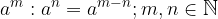
Pravilo za množenje potenc z enakimi eksponenti ugotovimo tako, da obe potenci najprej zapišemo kot produkt enakih faktorjev, nato različne faktorje med seboj pomnožimo in rezultat zapišemo s potenco.
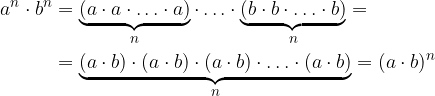
Potenci z enakima eksponentoma in različnima osnovama množimo tako, da osnovi pomnožimo, eksponent pa prepišemo:
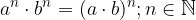
Pri deljenju potenc z enakimi eksponenti ravnamo podobno kot pri množenju.
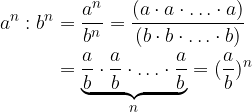
Potenci z enakima eksponentoma in različnima osnovama delimo tako, da osnovi delimo, eksponent pa prepišemo:
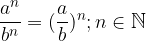
Potence potenciramo tako, da osnovo prepišemo, potenčne eksponente pa pomnožimo: