Osebne zbirke


Spoznali smo že kaj je potenca 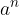 , kjer je n naravno število (glej gradivo potence s celimi eksponenti).
, kjer je n naravno število (glej gradivo potence s celimi eksponenti).
Na našo srečo tudi za potence z racionalnimi eksponenti veljajo enaka pravila, kot za potence s celimi eksponenti.
Naj bo 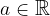 ;
; 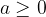 in
in 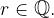 Med vsemi ulomki, ki predstavljajo racionalno število r, izberimo tistega, ki ima okrajšana števec in imenovalec.
Med vsemi ulomki, ki predstavljajo racionalno število r, izberimo tistega, ki ima okrajšana števec in imenovalec.
Recimo, da je ta ulomek 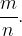 Tedaj velja:
Tedaj velja:
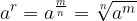
S tako definiranimi potencami računamo enako kot s potencami s celimi eksponenti.
Povzetek pravil za računanje s potencami z racionalnim eksponentom (pravila so v nadaljevanju podrobneje razložena) so povzeta v tabeli.
Naj bo 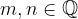 in
in 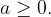 Potem velja:
Potem velja:
Potence z enakimi osnovami množimo tako, da osnovo prepišemo, potenčne eksponente pa seštejemo:
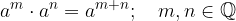
To trditev pokažemo tako, da za obe potenci uporabimo drug zapis potence (s koreni). Naj bosta:
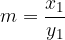
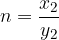
Potem velja:
Pri deljenju potenc z enakimi osnovami ravnamo podobno kot pri množenju.
Potence z enakimi osnovami delimo tako, da osnovo prepišemo, potenčne eksponente pa odštejemo:
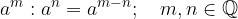
Pravila pri množenju in deljenju potenc z enakimi eksponenti so enaka kot pri potencah z naravnimi ekpsonenti.
Potenci z enakima eksponentoma in različnima osnovama množimo tako, da osnovi pomnožimo, eksponent pa prepišemo:
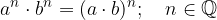
Potenci z enakima eksponentoma in različnima osnovama delimo tako, da osnovi delimo, eksponent pa prepišemo:
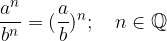
Potence potenciramo tako, da osnovo prepišemo, potenčne eksponente pa pomnožimo.
Pravilo za potenciranje potenc: