Osebne zbirke


Podobno, kot je množenje krajši zapis seštevanja, je potenca krajši zapis množenja enega števila.
V zapisu s potenco vidimo katero število imamo in kolikokrat ga množimo s samim sabo.
Množenje več enakih števil lahko zapišemo kot potenco.
Potenca je sestavljena iz dveh delov: osnove in stopnje. Zapišemo jo na naslednji način:
Osnova nam pove, katero število množimo samo s seboj, stopnja pa nam pove, koliko enakih števil množimo. Stopnjo imenujemo tudi eksponent.
Poleg števil lahko potenciramo tudi spremenljivke.
Števila in spremenljivke bomo pri potenciranju poimenovali s skupno besedo faktorji.
Osnova potence je faktor, ki ga množimo samega s seboj.
Stopnja ali eksponent potence je število faktorjev, ki jih množimo med seboj.
Tako osnova kot stopnja potence sta lahko tudi negativni števili.
Če je osnova potence negativna, jo zapišemo v oklepaj.
Spomnimo se, da ko množimo dve negativni števili, je rezultat pozitiven. Podobno je rezultat:
pozitiven vedno, ko med sabo množimo sodo mnogo negativnih števil,
negativen vedno, ko med sabo množimo liho mnogo negativnih števil.
Ugotovitev iz primera lahko posplošimo.
Če ima potenca z negativno osnovo liho stopnjo, potem je vrednost potence negativna.
Če ima potenca z negativno osnovo sodo stopnjo, je vrednost potence pozitivna.
Povedali smo, da potenca predstavlja množenje več enakih števil med seboj. Če potenciramo celoten produkt ali količnik, potem to pomeni, da med seboj zmnožimo enake produkte oziroma količnike.
Pri množenju potenc z enakimi osnovami osnovo prepišemo, stopnje pa seštejemo:
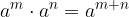
Pri deljenju potenc z enakimi osnovami osnovo prepišemo, stopnji pa odštejemo:
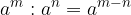
Oglejmo si še potenco s stopnjo 0. Zato izberimo primer deljenja enakih potenc - tako se bodo eksponenti odšteli v 0.
Gornji primer lahko posplošimo za poljubno osnovo, različno od 0.
Če poljubno neničelno število 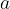 potenciramo z eksponentom 0, dobimo 1:
potenciramo z eksponentom 0, dobimo 1:

Potenca ima lahko tudi negativno stopnjo. V tem primeru minus v eksponentu razumemo tako, da potenciramo obratno vrednost osnove.
Kadar je stopnja potence negativna, potem vzamemo obratno vrednost osnove in to na pozitivno potenco.
Poglejmo potenco 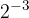 . Obratna vrednost od osnove 2 je ulomek
. Obratna vrednost od osnove 2 je ulomek  , zato lahko zapišemo:
, zato lahko zapišemo:
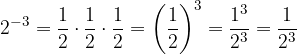
Poglejmo si gornjo enakost še v drugo smer.
Potenco z negativno stopnjo 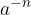 zapišemo kot ulomek, v katerem je števec enak 1, imenovalec pa
zapišemo kot ulomek, v katerem je števec enak 1, imenovalec pa 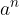 :
:
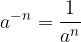
Ko množimo potenci z enakima stopnjama, osnovi pomnožimo, stopnjo pa prepišemo.
Pri deljenju potenc z enakima stopnjama osnovi delimo, stopnjo pa prepišemo.
Pri množenju potenc z enakima stopnjama osnovi pomnožimo, stopnjo pa prepišemo:
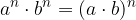
Pri deljenju potenc z enakima stopnjama osnovi delimo, stopnjo pa prepišemo:
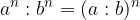
Produkt potenciramo tako, da potenciramo vse faktorje, ki nastopajo v produktu.
Količnik potenciramo tako, da potenciramo posebej deljenec in posebej delitelj.
Produkt potenciramo tako, da potenciramo vse faktorje, ki nastopajo v produktu:
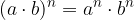
Količnik potenciramo tako, da potenciramo posebej deljenec in posebej delitelj:
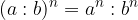
Količnik je ulomek, zato velja tudi naslednja trditev:
Ulomek potenciramo tako, da posebej potenciramo števec in imenovalec:
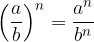
Potence lahko tudi potenciramo. Pri potenciranju potenc osnovo prepišemo, stopnji pa pomnožimo.
Pri potenciranju potenc osnovo prepišemo, stopnji pa pomnožimo:
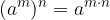
Do sedaj smo se naučili, da ima v računskih izrazih množenje in deljenje prednost pred seštevanjem in odštevanjem. Potence pa prevzamejo prednost pred vsemi štirimi operacijami.
Če v izrazu ni oklepajev, računamo po naslednjem vrstnem redu:
potence
množenje in deljenje
seštevanje in odštevanje
Oklepaj ima ne glede na pomembnost posamezne računske operacije vedno prednost pred vsemi. Enako velja tudi v računskih izrazih s potencami.
Če v izrazu nastopajo oklepaji, računamo po naslednjem vrstnem redu:
oklepaji
potence
množenje in deljenje
seštevanje in odštevanje
Kvadriranje je potenciranje, pri katerem je stopnja potence vedno enaka 2.
Potenco števila s stopnjo 2 imenujemo kvadrat števila.
Pri kvadriranju število pomnožimo samo s seboj, zato je ne glede na predznak števila rezultat vedno pozitiven.
Posebnost je število 0. Če tega zmnožimo samega s seboj, je rezultat enak 0.
Kvadrat števila, različnega od 0, je vedno pozitivno število.
Kvadrat števila 0 je enak 0.
Kvadrat števila je enak kvadratu njegovega nasprotnega števila.
S pomočjo pravil za potenciranje si lahko poenostavimo tudi izračun kvadratnega korena:
celih števil, ki se končajo z ničlami in
decimalnih števil.
Postopka si oglejmo v naslednjih dveh primerih.
Naravno število, ki se konča z ničlami, kvadriramo tako, da:
zapišemo kvadrat tistega dela števila, ki nima ničel,
na desni strani dopišemo dvojno število ničel.
Decimalno število kvadriramo tako, da:
zapišemo kvadrat števila brez upoštevanja decimalne vejice,
nato pa decimalno vejico postavimo tako, da bo število decimalk dvojno glede na število, ki smo ga kvadrirali.