Prijava z e-naslovom
Prijava brez gesla
Poligon za rolkanje (skejtpark) se začenja s krožnim gladkim delom s polmerom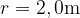 
. Krožnemu delu sledi pas bolj hrapave podlage z dolžino 
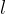in klanec z naklonskim kotom 
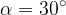(slika). Z vrha poligona (točka A) se spusti rolkar z maso 
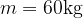in se med vožnjo ne poganja.
Rolkar na progi.
Kolikšna je potencialna energija rolkarja v točki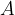 
, če privzamemo, da je potencialna energija v najnižji točki enaka nič?
Kolikšna je hitrost rolkarja v točki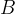 
, ki je na sredini med točkama 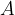in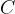 
?
Na sliki spodaj je krožni del poligona. Nariši zunanje sile na rolkarja ko je v točki 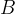in jih poimenuj.
Rolkar na sredini med mestoma in .
Izračunaj silo, s katero podlaga deluje na rolkarja ko je v točki .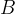
Izračunaj hitrost s katero se rolkar pripelje na hrapavi vodoravni del poligona?
Gibanje rolkarja na hrapavem vodoravnem delu poligona zavira sila trenja. Ta del rolkar prevozi v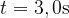 
; hitrost rolkarja se na tem delu enakomerno zmanjša na tretjino največje dosežene hitrosti.
Nariši graf spreminjanje hitrosti rolkarja s časom.
Izračunaj dolžino hrapavega dela poligona.
Kolikšen je koeficient trenja na hrapavem delu poligona?
Rolkar se pripelje do vznožja klanca. Koeficient trenja je enak kot na vodoravnem delu poligona.
Ali rolkar pri vožnji po klancu navzgor, doseže višino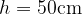 
? Odgovor utemelji z računom!
