Prijava z e-naslovom
Prijava brez gesla
Pravilni n-kotnik je geometrijski lik z n oglišči, n enako dolgimi stranicami in n skladnimi koti.
Pravilni 20-kotnik.
Pravilni n-kotnik je poseben primer splošnega n-kotnika, ki za razliko od pravilnega n-kotnika stranic in kotov nima nujno skladnih.
Diagonala je daljica, ki povezuje nesosednja oglišča n-kotnika.
Vsako oglišče v n-kotniku ima dve sosednji oglišči in (n-3) oglišč, ki niso sosednja.
Splošen izraz za izračun števila diagonal (velja tudi za nepravilne n-kotnike) se glasi:
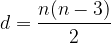
pri čemer n pomeni število stranic n-kotnika.
Diagonale izbočenega večkotnika se nahajajo vedno v notranjosti le-tega.
Pravilni n-kotnik ima n notranjih kotov, ki so enake velikosti.
Splošen izraz za izračun vsote notranjih kotov izbočenih (konveksnih) n-kotnikov (tudi nepravilnih) se glasi:
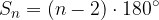
pri čemer n pomeni število stranic n-kotnika.
V pravilnem n-kotniku lahko izračunamo tudi velikost posameznega notranjega kota:
Velikost posameznega notranjega kota v pravilnem n-kotniku dobimo tako, da vsoto notranjih kotov delimo s številom stranic n-kotnika:
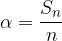
Pravilni n-kotnik ima n zunanjih kotov, ki so enake velikosti.
Vsota zunanjih kotov izbočenih (konveksnih) n-kotnikov (tudi nepravilnih) je vedno enaka in sicer znaša 360°.
V pravilnem n-kotniku lahko izračunamo tudi velikost posameznega zunanjega kota:
Velikost posameznega zunanjega kota v pravilnem n-kotniku dobimo tako, da vsoto zunanjih kotov delimo s številom stranic n-kotnika:
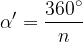
Enačba za obseg n-kotnika se glasi:
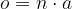
pri čemer n predstavlja število stranic, a pa je osnovnica n-kotnika.
N-kotnik sestavlja n skladnih enakokrakih trikotnikov, zato je njegova ploščina enaka n-kratniku ploščine enega enakokrakega trikotnika:
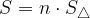
Ob upoštevanju enačbe za ploščino enakokrakega trikotnika ob podani dolžini kraka in kotu med krakoma (za izpeljavo glej spodnji primer) dobimo naslednjo enačbo:
Enačba za ploščino n-kotnika se glasi:
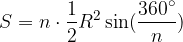
pri čemer n predstavlja število stranic n-kotnika, R pa je radij n-kotniku očrtanega kroga
