Osebne zbirke


Če želimo določiti lego poljubne točke moramo poznati pravokotni koordinatni sistem. Od tega kje se točka nahaja (ali v ravnini ali v prostoru) pa je odvisno kateri pravokotni koordinatni sistem bomo uporabili.
V tem poglavju se bomo posvetili točkam v prostoru. Za določitev njihove lege, pa moramo poznati pravokotni koordinatni sistem v prostoru, ki ga narišemo po naslednjem postopku:
V prostoru si izberemo poljubno točko in jo označimo z 0. Točko 0 imenujemo koordinatno izhodišče.
Sedaj narišemo tri premice, ki so paroma pravokotne.
Premice orientiramo po sistemu desnosučnega pravila, kot kaže slika.
Izberemo si enoto in z njo opremimo vse tri premice, da dobimo številske osi, ki jih imenujemo koordinatne osi.
Koordinatne osi poimenujemo. Prvi dve poznamo že iz pravokotnega sistema v ravnini, to sta os x ali abscisna os in os y ali ordinatna os, tretja pa je os z ali aplikatna os.
Položaj točke T glede na tako izbran koordinatni sistem zapišemo s tremi koordinatami 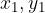 in
in 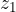 , pri čemer je
, pri čemer je 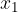 prva koordinata točke T in nam pove odsek na x oziroma abscisni osi,
prva koordinata točke T in nam pove odsek na x oziroma abscisni osi, 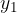 druga koordinata točke T in nam pove odsek na y oziroma ordinatni osi in
druga koordinata točke T in nam pove odsek na y oziroma ordinatni osi in 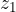 tretja koordinata točke T in nam pove odsek na z oziroma aplikatni osi.
tretja koordinata točke T in nam pove odsek na z oziroma aplikatni osi.
Lega točke T, ki jo zapišemo kot urejeno trojko 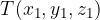 je tako natanko določena in ni enaka kot
je tako natanko določena in ni enaka kot 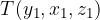 . Če znotraj urejene trojke zamenjamo vrstni red koordinat dobimo različne točke.
. Če znotraj urejene trojke zamenjamo vrstni red koordinat dobimo različne točke.
Poglejmo si primer točke in množice točk v prostoru: