Prijava z e-naslovom
Prijava brez gesla
Naravna števila, ki so deljiva zgolj z 1 in s samim seboj, imenujemo praštevila. Vsa ostala naravna števila (razen 1) pa so sestavljena števila.
Število 1 je posebnost, saj ni ne praštevilo, ne sestavljeno število.
Števila, ki imajo natanko dva delitelja (1 in samega sebe), imenujemo praštevila.
Števila, ki imajo več deliteljev, imenujemo sestavljena števila.
Število 1 ima le enega delitelja, zato ni ne praštevilo ne sestavljeno število.
Zapišimo prvih nekaj praštevil.
Praštevila lahko opazujemo tudi z vidika ploščine. Vemo da ploščino pravokotnika izračunamo kot produkt dveh števil - širine in dolžine. Poljubno praštevilo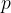 
pa lahko kot produkt naravnih števil zapišemo le na en način:
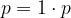
Če si torej zamislimo neko ploščino 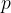s praštevilsko vrednostjo, je z naravnimi števili nikakor ne moremo zapisati kot produkt dveh naravnih števil, od katerih bi bili obe večji od 1.
Zato ploščina v vrednosti praštevila nikoli ne more predstavljati pravokotnika s širino stranic večjo od 1:
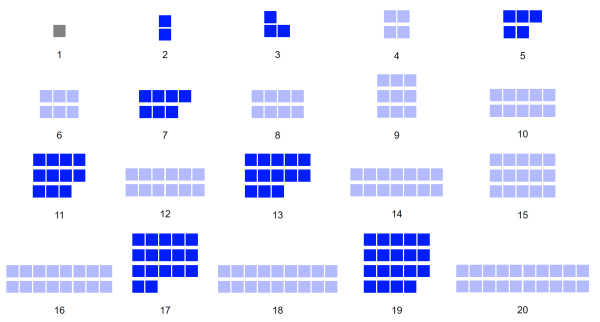
Ploščine, ki niso praštevila, lahko upodobimo s pravokotniki, pri katerih sta obe stranici večji od 1. Praštevilskih ploščin pa ne moremo narisati kot pravokotnik, ki bi imel obe stranici večji od 1.
Število 2 je edino sodo praštevilo. Vsa ostala soda števila so večja in imajo zato več kot dva delitelja, torej najmanj naslednje delitelje: 1, 2, samega sebe ...
Poglejmo eno metodo, kako iz prvih nekaj števil presejmo samo praštevila.
Kot smo videli v primeru z Eratostenovim sitom, so praštevila posejana vedno bolj redko, ko gremo proti večjim številom. Med večjimi števili je vse več večkratnikov manjših praštevil (2, 3, 5 ...)
Kljub temu, da so večja praštevila na številski premici posejana bolj na redko, jih je še vedno neskončno, saj je številska premica neskončna.
Vsako število lahko zapišemo v obliki produkta. Če v produktu nastopajo samo praštevila, smo število razcepili na prafaktorje. Če nek prafaktor v zapisu nastopa večkrat, ga lahko zapišemo v obliki potence in tako skrajšamo zapis.
Prafaktorje poljubnega sestavljenega števila dobimo z razstavljanjem. To lahko storimo na več načinov, najpogosteje:
z zapisom deljenja s praštevili (v stolpcu) ali
z razcepom v obliki drevesa.
