Osebne zbirke

Premica je neomejena ravna črta. Premico označimo z malo tiskano črko (p, r, s, t,...):
Relacijo z matematičnimi simboli zapišemo kot
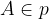
Točke, ki ležijo na isti premici, so kolinearne:
Relacijo z matematičnimi simboli zapišemo kot
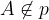
Vzporedni premici nimata nobene skupne točke.
Relacijo z matematičnimi simboli zapišemo kot
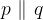
Poseben primer vzporednosti sta premici, ki sovpadata. Taki premici imata neskončno skupnih točk.
Sovpadanje premic z matematičnimi simboli zapišemo kot:
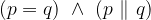
Premici, ki se sekata, imata natanko eno skupno točko, ki jo imenujemo presečišče:
Premici, ki se sekata, z matematičnimi simboli zapišemo kot
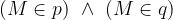
pri čemer je točka M presečišče premic p in q.
Premici, ki se sekata, imenujemo sečnici.
Poltrak je ravna črta, ki je na eni strani neomejena, na drugi strani pa jo omejuje točka. To točko imenujemo izhodišče poltraka. Poltrak označimo z malo tiskano črko (h, k, l,...):
Poltrak, ki poteka skozi točko, lahko označimo tudi s parom velikih tiskanih črk (AB, CD, EF,...), pri čemer prva črka vedno predstavlja izhodišče, druga pa točko, skozi katero gre poltrak:
Daljica je ravna črta, ki je na obeh konceh omejena s točkama. Ti dve točki imenujemo krajišči daljice. Daljico poimenujemo po njenih krajiščih - označimo jo s parom velikih tiskanih črk (AB, CD, EF,...):
Ko govorimo o razdalji med točkama, mislimo na najkrajšo razdaljo med njima.
Najkrajšo razdaljo med krajiščema daljice imenujemo dolžina daljice.
Dolžino daljice s krajišči E in F z matematičnimi simboli zapišemo: 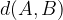 .
.
Več o razdalji med točkama si lahko preberete v poglavju Razdalja med dvema točkama v ravnini.
Simetrala daljice je premica, ki razpolavlja daljico in oklepa z njo pravi kot.
Na spodnji sliki je simetrala označena z malo tiskano črko s, točka M pa je presečišče daljice AB:
Simetralo daljice bomo potrebovali pri načrtovanju trikotniku očrtanega kroga.