Osebne zbirke
Prijava z e-naslovom
Prijava brez gesla
Količine so lahko medsebojno odvisne.
Odnosov med odvisno in neodvisno količino je več vrst, eden izmed njih je premo sorazmerje.
Če se pri:
dvakratnem, trikratnem ...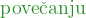 
prve količine
tudi druga količina dvakrat, trikrat ... 
,
potem sta ti dve količini v premem sorazmerju.
Enako velja tudi v obratni smeri. Če se pri:
dvakratnem, trikratnem ... 
prve količine
tudi druga količina dvakrat, trikrat ... 
,
potem sta ti dve količini v premem sorazmerju.
Če sta količini med seboj odvisni, nista nujno v premem sorazmerju.
Spomnimo se, kaj sta odvisna in neodvisna spremenljivka.
Količino, ki jo lahko poljubno izberemo ali spremenimo, imenujemo neodvisna spremenljivka. Običajno jo označimo z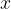 
.
Količina, ki se prilagaja drugi količini in je ne moremo poljubno izbirati, imenujemo odvisna spremenljivka. Običajno jo označimo z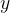 
.
V situaciji iz prejšnjega primera imamo dve spremenljivki:
Število vstopnic za koncert je neodvisna spremenljivka, saj je število vstopnic lahko poljubno.
Cena, ki jo plačamo za vstopnice, pa je odvisna spremenljivka, saj je odvisna od števila vstopnic.
Vpišimo v tabelo ceno 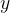za eno, dve, tri in štiri vstopnice :
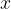Iz tabele razberemo, da je cena vedno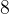 
-kratna vrednost števila vstopnic.
Izrazimo količnik med ceno 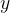in številom vstopnic :
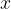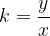
Količnik je vedno enak, ne glede na to, katero vrstico tabele gledamo. V matematiki število, ki se ne spreminja, imenujemo konstanta.
Kadar sta količini premo sorazmerni, njun količnik imenujemo koeficient premega sorazmerja.
Koeficient k premega sorazmerja je količnik med odvisno in neodvisno spremenljivko v premem sorazmerju:
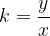
Koeficient premega sorazmerja je konstanta. V vseh vrsticah ima enako vrednost.
Če iz zapisa koeficienta premega sorazmerja
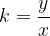
izrazimo odvisno spremenljivko 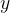, dobimo enačbo premega sorazmerja:
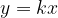
pri čemer:
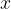predstavlja neodvisno spremenljivko,
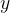predstavlja odvisno spremenljivko,
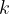pa je koeficient premega sorazmerja.
Enačba premega sorazmerja je:
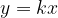
Kadar imamo dve količini v premem sorazmerju, lahko namesto zamudnega merjenja obeh količin izmerimo zgolj eno, drugo pa izračunamo po enačbi ali s sklepanjem.
Premo sorazmerje neodvisne količine 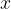in odvisne količine 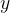v obliki enačbe zapišemo kot
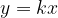
pri čemer je 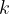koeficient premega sorazmerja.
Če želimo izračunati vrednost neznane količine 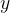, preprosto vstavimo 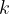in 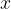v zgornjo enačbo in ju zmnožimo.
Če 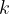ni podan, ga izračunamo iz znanih podatkov.
Če želimo izračunati vrednost neznane količine 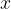, jo je potrebno najprej izraziti iz enačbe premega sorazmerja:
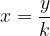
Vemo, da se pri premem sorazmerju z dvakratnem, trikratnem ... povečanju prve količine dvakrat, trikrat ... poveča tudi druga količina.
Enako velja tudi v obratni smeri. Z dvakratnim, trikratnim ... zmanjšanjem prve količine se dvakrat, trikrat ... zmanjša tudi druga količina.
To z drugimi besedami pomeni, da se pri množenju prve količine z nekim številom istočasno pomnoži tudi vrednost druge količine. Enako velja za deljenje. Če prvo količino delimo z nekim številom, se istočasno z istim številom deli tudi druga količina.
Še enkrat si oglejmo tabelo s ceno vstopnic iz zgornjega primera:
Naredimo nekaj izračunov za preizkus zgornje trditve:
Če podvojimo število vstopnic 2 v drugi vrstici tabele, dobimo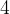 
vstopnice v četrti vrstici. Istočasno se podvoji tudi cena iz 
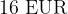na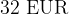 
.
Če ceno v četrti vrstici tabele 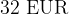, delimo s 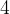, dobimo 
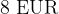v prvi vrstici. Istočasno se s 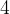deli tudi število vstopnic, iz 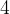na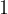 
.
S sklepanjem pridemo do rezultata postopoma:
najprej z deljenjem obeh vrednosti v isti vrstici tabele izračunamo vrednost prve spremenljivke za eno enoto druge spremenljivke,
nato pa z množenjem obeh vrednosti v isti vrstici tabele izračunamo vrednost prve spremenljivke za želeno število enot druge spremenljivke.
Pri tej metodi računanja količin se izognemo računanju koeficienta 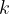premega sorazmerja.
Izračunajmo primera iz prejšnjega poglavja še s pomočjo sklepanja. S tem nam ne bo potrebno izračunati koeficienta 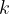premega sorazmerja.
