Osebne zbirke


Pri meritvah v tehniki in naravoslovju nam merilni instrumenti običajno ne omogočajo merjenja natančnih vrednosti merjenih količin. Zadovoljiti se moramo s približnimi vrednostmi. Pogosto smo prisiljeni računati s približki, saj točnih vrednosti niti ne poznamo.
Pri merjenju se srečamo z dvema vrednostma, ki ju različno označimo. In sicer:
približna vrednost izmerjene količine, ki jo označimo z A
točna vrednost izmerjene količine, ki jo označimo z a
Glede na vrsto napake ločimo dve napaki:
Z absolutno napako izrazimo absolutni meji, znotraj katerih verjetno leži prava vrednost merjene količine. Torej:
Z absolutno napako izrazimo velikost napake, ki smo jo storili:
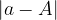
Velja tudi, če z  označimo največjo možno vrednost za absolutno napako, potem je točna vrednost omejena z
označimo največjo možno vrednost za absolutno napako, potem je točna vrednost omejena z
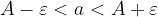
ali zapisano drugače
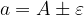
Ta zapis razumemo tako, da je a največ 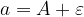 in najmanj
in najmanj 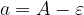 .
.
Opomba:  je grška črka epsilon.
je grška črka epsilon.
Pri računanju s približki velja za absolutno napako pravilo:
Naj bosta a in b točni vrednosti izmerjene količine in naj bosta A in B pripadajoča približka.
Potem je absolutna napaka vsote (razlike) manjša ali enaka vsoti absolutnih napak seštevancev:
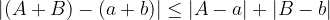
Pogosto nas pri ocenjevanju napak bolj kot velikost napake zanima njeno razmerje s točno vrednostjo. Dobljeno razmerje imenujemo relativna napaka. Torej:
Z relativno napako izrazimo natančnost meritve in je enaka:
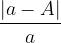
Relativno napako običajno izrazimo v odstotkih in jo označimo s črko r.
Pri računanju s približki veljata za relativno napako pravili:
Naj bosta a in b točni vrednosti izmerjene količine in naj bosta A in B pripadajoča približka. Potem velja:
Relativna napaka zmnožka je manjša ali enaka vsoti relativnih napak faktorjev:

Relativna napaka kvocienta je vsota relativnih napak števca in imenovalca
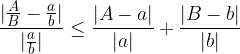
Zaokroževanje uporabljamo, kadar ne potrebujemo povsem natančnih rezultatov. Z vsakim zaokroževanjem nastanejo približki. Pri vsakem naslednjem približku je napaka večja ali enaka.
Velja naslednje pravilo:
če je prva odvržena števka 0,1,2,3 ali 4, obdržane števke ostanejo nespremenjene
če je prva odvržena števka 5,6,7,8 ali 9, zadnjo obdržano števko povečamo za 1
Opomba: Če je zadnja obdržana števka 9 , je treba za 1 povečati tudi prejšnjo števko.
Ločimo dve vrsti zaokroževanja:
Zaokroževanje na n-mest natančno:
Število je zapisano na n-mest natančno, če ima v svojem zapisu n-števk, pri tem ničel pred prvo neničelno števko ne štejemo.
Zaokroževanje na n-decimalk natančno:
Število je zapisano na n-decimalk natančno, če ima v svojem zapisu za decimalno vejico n-števk. Pri tem se štejejo tudi vse ničle za decimalno vejico, ne glede ali je pred njimi kakšna neničelna števka.
Opomba: pri seštevanju, odštevanju, deljenju in množenju ponavadi rezultat zaokrožimo na toliko decimalnih mest kot jih ima faktor z najmanj decimalnih mest.