Prijava z e-naslovom
Prijava brez gesla
Prizma je geometrijsko telo, ki ima površje sestavljeno iz več oglatih ravnih ploskev. Dve izmed ploskev sta vedno:
vzporedni
in skladni.
Imenujemo ju osnovni ploskvi. Ostale ploskve so stranske ploskve.
Prizme delimo na dve veliki skupini:
pokončne - osnovni ploskvi ležita ena pod drugo,
poševne - osnovni ploskvi za zamaknjeni.
V naravi se oblika poševne prizme pogosto pojavlja v kristalih in mineralih.
Kot smo videli, obstaja več vrst prizem, vsem pa lahko pripišemo nekaj skupnih lastnosti.
Prizma je oglato geometrijsko telo, omejeno z:
dvema osnovnima ploskvama
plaščem
Stranske ploskve sestavljajo plašč prizme.
a) osnovni ploskvi prizme, b) plašč prizme
Za vsako prizmo so značilni naslednji elementi:
Osnovni ploskvi sta skladna in vzporedna n-kotnika.
Stranske ploskve so paralelogrami, ki sestavljajo plašč prizme. Plašč je sestavljen iz n paralelogramov.
Osnovni robovi so stranice osnovnih ploskev.
Stranski robovi so vsi ostali robovi prizme. Med seboj so skladni in vzporedni.
Višina prizme je razdalja med ravninama, na katerih se nahajata osnovni ploskvi. Višina je daljica, ki je pravokotna na obe osnovni ploskvi.
Značilni elementi prizme
Zgornje opredelitve veljajo za vsako prizmo, tudi za poševno.
Videli smo, da razlikujemo pokončne in poševne prizme. Poglejmo si, kdaj je prizma pokončna in katere značilnosti ima v tem primeru.
Prizma je pokončna, če so stranski robovi pravokotni na osnovno ploskev. To pa pomeni, da so stranske ploskve v pokončni prizmi pravokotniki, saj so vsi koti stranske pleskve pravi (90°). Ker je na osnovno ploskev pravokotna tudi višina, so:
višina
in vsi stranski robovi
med seboj vzporedni.
Značilni elementi pokončne prizme
Za pokončno prizmo veljajo naslednje posebnosti:
Stranske ploskve so pravokotniki. Zato je tudi plašč pravokotnik.
Višina pokončne prizme je skladna s stranskimi robovi.
Omenjene poenostavitve nam olajšajo računanje površine in prostornine prizme, ki ju bomo spoznali v nadaljevanju.
Površina prizme je vsota ploščin vseh njenih mejnih ploskev. Mejne ploskve prizme so večkotniki, katerih ploščine lahko izračunamo.
Celotna površina prizme pa je razporejena po več ravninah. Da si površino lažje predstavljamo, mejne ploskve razgrnemo na eno ravnino.
Če mejne ploskve prizme razgrnemo na ravnino, dobimo mrežo prizme. Celotna mreža predstavlja sestavljen geometrijski lik.
Mreža pokončne tristrane prizme
Mejne ploskve telesa, razgrnjene na ravnino, imenujemo mreža geometrijskega telesa.
Računanje površine prizme si lahko predstavljamo kot računanje ploščine sestavljenega geometrijskega lika. Pri tem:
najprej izračunamo ploščine posameznih delov,
nato pa te ploščine seštejemo.
V osnovni šoli računamo le površine pokončnih prizem.
Zgradba prizme nam omogoča, da si računanje površine nekoliko poenostavimo, saj sta osnovni ploskvi enako veliki. Pokončna prizma pa ima še dodatno prednost pri računanju - vse stranske ploskve lahko združimo v en velik pravokotnik (glej sliko zgoraj: Mreža pokončne tristrane prizme).
Osnovni ploskvi v pokončni prizmi sta lahko poljubna skladna n-kotnika. Zato za računanje njunih ploščin ni enotne formule. Lahko pa zapišemo:
Ploščino osnovne ploskve prizme označimo z O.
Izračunamo jo enako, kot ploščino n-kotnika.
Kot smo že povedali, ima plašč pokončne prizme obliko pravokotnika, v katerem so vsebovane vse stranske ploskve prizme. Ta pravokotnik ima:
eno stranico enako obsegu osnovne ploskve
druga pa je enaka višini prizme.
Splošna enačba za ploščino plašča pl pokončne prizme se glasi:
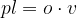
pri čemer je o obseg osnovne ploskve, v pa višina prizme.
Celotno površino prizme dobimo tako, da seštejemo obe osnovni ploskvi in plašč.
Splošna enačba za površino P prizme se glasi:
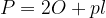
pri čemer je O ploščina osnovne ploskve, pl pa ploščina plašča prizme.
Prostornina prizme je velikost prostora, ki ga prizma zavzame.
Celotno prostornino prizme opišemo tako, da osnovno ploskev premaknemo vzdolž višine. Za vsa telesa, ki jim opišemo prostornino po omenjenem postopku, izračunamo prostornino po spodnjem obrazcu:
Splošna enačba za izračun prostornine V prizme se glasi:
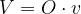
pri čemer je O ploščina osnovne ploskve, v pa višina prizme.
Prizme ločimo po njihovih lastnostih. Poglejmo si kriterije ločevanja.
Kot smo spoznali že v uvodu, so prizme lahko pokončne ali poševne. Poševne prizme tukaj ne obravnavamo podrobneje.
Prizmo poimenujemo glede na n-kotnik, ki predstavlja osnovno ploskev.
Splošno lahko zapišemo:
Prizma, katere osnovna ploskev je n-kotnik, se imenuje n-strana prizma.
Osredotočimo se na robove prizme. Posebne primere predstavljajo prizme, ki imajo skladne:
osnovne robove,
vse robove v prizmi.
Prizmo, ki ima enako dolge osnovne robove, poimenujemo pravilna prizma.
Osnovni robovi predstavljajo stranice osnovne ploskve. Mnogokotnik z enako dolgimi stranicami je pravilen, zato podobno zapišemo tudi za prizmo:
Prizma je pravilna, če ima za osnovno ploskev pravilni n-kotnik.
Če ima prizma enako dolge vse robove (tako osnovne kot stranske), jo imenujemo enakoroba prizma.
Prizma je enakoroba, če ima vse robove enako dolge.
Za enakorobo prizmo lahko zapišemo tudi naslednje:
Prizma, ki je enakoroba, je hkrati tudi pravilna.
Za posebne primere prizem veljajo poenostavljeni obrazci za izračun površine in prostornine. Izpeljemo jih iz osnovnih formul ob upoštevanju lastnosti posamezne prizme.
Podrobneje si bomo ogledali nekaj primerov:
tristranih,
štiristranih
pokončnih prizem.
Posebna primera štiristranih prizem predstavljata kvader in kocka. Najprej pa si poglejmo tristrane prizme.
Pravilna tristrana pokončna prizma ima za osnovno ploskev enakostranični trikotnik:
Pravilna tristrana prizma v poševni projekciji
Površina
Za lažji izračun površine narišimo mrežo prizme:
Mreža pravilne tristrane prizme
Ploščina osnovne ploskve pravilne tristrane prizme je enaka ploščini enakostraničnega trikotnika:
Enačba za ploščino osnovne ploskve pravilne tristrane prizme se glasi:
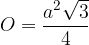
pri čemer je a dolžina osnovnega roba prizme.
Ena stranica pravokotnika v plašču je enaka obsegu osnovne ploskve, druga pa višini prizme:
Mreža pravilne tristrane prizme, plašč je označen z modro barvo
Ker je osnovna ploskev enakostranični trikotnik, je njegov obseg trikratnik osnovnice:
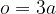
Ob upoštevanju splošne enačbe za ploščino plašča pokončne prizme
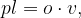
velja za plašč pravilne tristrane prizme spodnji obrazec.
Enačba za ploščino plašča pl pravilne tristrane pokončne prizme se glasi:
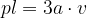
pri čemer je a dolžina osnovnega roba, v pa višina prizme.
Ob upoštevanju splošne enačbe za površino prizme
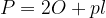
zapišemo:
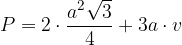
Ko izraz okrajšamo in uredimo, lahko zapišemo enačbo za celotno površino:
Enačba za površino P pravilne tristrane pokončne prizme se glasi:
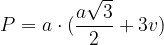
pri čemer je a dolžina osnovnega roba, v pa višina prizme.
Prostornina
Pri računanju površine prizme smo že ugotovili, da je osnovna ploskev pravilne tristrane prizme enakostranični trikotnik s ploščino:
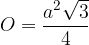
Zgornjo enačbo vstavimo v splošno enačbo za izračun prostornine prizme:
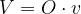
in dobimo spodnji obrazec.
Enačba za izračun prostornine V pravilne tristrane pokončne prizme se glasi:
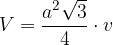
pri čemer je a dolžina osnovnega roba, v pa višina prizme.
Če je štiristrana prizma hkrati tudi pokončna, so vse njene ploskve (osnovni in stranske) pravokotniki:
Kvader v poševni projekciji
Štiristrano pokončno prizmo imenujemo kvader.
Kvader je podrobneje obravnavan v gradivu Kvader. Tukaj pa si poglejmo še, kako do enakih formul za:
površino,
prostornino
kvadra pridemo preko obrazcev, ki veljajo za vsako prizmo.
Površina
Za lažjo predstavo si najprej poglejmo mrežo kvadra:
Mreža kvadra
Do formule za površino kvadra bomo prišli preko splošne formule za površino prizme:
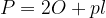
Dobili jo bomo tako, da v zgornjo formulo vstavimo ploščini:
osnovne ploskve O,
plašča pl.
Zapišimo najprej njuni formuli:
ploščina osnovne ploskve kvadra
Upoštevamo, da je osnovna ploskev kvadra pravokotnik z dolžino a in širino b. Ploščino osnovne ploskve zato izračunamo kot ploščino pravokotnika:
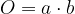
ploščina plašča kvadra
Tudi plašč kvadra je pravokotnik. Stranici v plašču pa sta:
obseg osnovne ploskve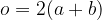 
,
višini kvadra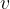 
.
Ploščina plašča se glasi:
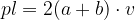
Izpeljimo formulo za izračun površine kvadra:
Dobili smo splošno formulo za izračun površine kvadra.
Enačba za površino kvadra se glasi:
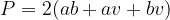
pri čemer je a dolžina osnovne ploskve, b je širina osnovne ploskve, v pa višina kvadra.
Prostornina
Izpeljimo še formulo za prostornino kvadra s splošno formulo za prostornino prizme:
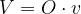
Izpeljimo jo:
Prišli smo do formule za prostornino kvadra, kot jo že poznamo.
Enačba za izračun prostornine kvadra se glasi:
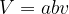
pri čemer je a dolžina osnovne ploskve, b širina osnovne ploskve, v pa višina kvadra.
Če je štiristrana prizma tako pokončna kot enakoroba, so vse njene ploskve (osnovni in stranske) kvadrati:
Kocka v poševni projekciji
Enakorobo štiristrano pokončno prizmo imenujemo kocka.
Do formul za površino in prostornino kocke, ki jih že poznamo, bomo prišli tudi preko obrazcev, ki veljajo za vse prizme:
Površina
Za izračun površine nam pri predstavi pomaga mreža kocke:
Mreža kocke
Izpeljimo formulo za površino kocke s splošno formulo za površino prizme:
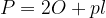
Dobili jo bomo tako, da v zgornjo formulo vstavimo ploščini:
osnovne ploskve kocke
Upoštevamo, da je osnovna ploskev kocke kvadrat z dolžino stranice a. Ploščina osnovne ploskve se glasi:
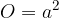
plašča kocke
Tudi plašč kocke je pravokotnik. Stranici plašča sta:
obsegu osnovne ploskve o = 4a
višini kocke a
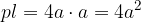
Izpeljimo formulo za površino kocke:
Dobili smo formulo za izračun površine kocke, ki jo že poznamo.
Enačba za površino kocke se glasi:
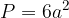
pri čemer je a dolžina osnovnega roba kocke.
Prostornina
Izpeljimo formulo za prostornino kocke s splošno formulo za prostornino prizme:
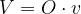
Izpeljimo jo:
Dobili smo formulo za izračun prostornine kocke, ki jo tudi že poznamo.
Enačba za izračun prostornine kocke se glasi:
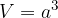
pri čemer je a dolžina osnovnega roba kocke.
