Osebne zbirke


Produkt vsote in razlike dveh enakih členov je le poseben primer množenja dvočlenikov. Ker ga pri računanju pogosto srečamo, si ga poglejmo malce podrobneje. Kot bomo videli, lahko ta produkt izračunamo enostavneje in hitreje kot produkt poljubnih dvočlenikov.
Najprej zapišimo vsoto in razliko dveh enakih členov.
Zapišimo še produkt vsote in razlike enakih členov.
Poglejmo si, po kakšnem pravilu se izračuna zgornji produkt.
Produkt vsote in razlike dveh enakih členov izračunamo po enakem postopku kot se množijo veččleniki.
Iz zgornjega primera sklepamo, da v rezultatu produkta vsote in razlike dveh enakih členov ostane le razlika:
kvadrata prvega in
kvadrata drugega člena.
Izpeljimo še splošno formulo za računanje produkta poljubnih členov 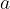 in
in 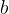 .
.
Člena 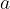 in
in 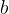 sta poljubna, zato zgornji rezultat velja splošno - ne glede na to, kakšne člene vstavimo namesto
sta poljubna, zato zgornji rezultat velja splošno - ne glede na to, kakšne člene vstavimo namesto 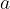 in
in 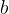 .
.
Vidimo, da pri produktu vsote in razlike poljubnih dveh enakih členov dobimo dvočlenik. Ta dvočlenik pa je vedno razlika kvadratov prvega in drugega člena.
Zapišimo zgornjo ugotovitev v obliki splošne formule za produkt med vsoto in razliko dveh enakih členov.
Produkt vsote in razlike dveh enakih členov a in b izračunamo po pravilu:
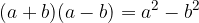
Pri tem dobimo razliko kvadratov prvega in drugega člena.