Osebne zbirke


V tem gradivu si bomo pogledali osnovne računske operacije z ulomki. To so:
seštevanje
odštevanje
množenje
deljenje
Nato pa si bomo ogledali še vse, kar lahko z ulomki počnemo pod pogojem, da ta ne spremeni svoje vrednosti. S tem imamo v mislih predvsem:
razširjanje ulomkov in
krajšanje ulomkov.
Vsako od zgoraj naštetih dejanj bomo obravnavali ločeno:
Princip seštevanja ulomkov razdelimo na dve točki, glede na imenovalec.
Ulomka imata enak imenovalec
Če imata ulomka enak imenovalec ju seštejemo tako, da seštejemo samo njuna števca, imenovalec pa prepišemo. Torej velja:
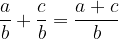
Ulomka imata različen imenovalec
Če imata ulomka različna imenovalca, ju moramo najprej razširiti na skupni imenovalec. Torej velja:
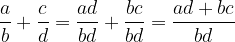
Za seštevanje ulomkov veljata naslednja dva zakona:
Komutativnost je zakon o zamenjavi. Torej dva ulomka sta komutativna kadar:
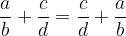
Asociativnost je zakon o združevanju. Seštevanje je asociativna operacija, torej velja:
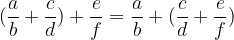
Za odštevanje velja podobno kot za seštevanje. Torej bomo tudi tukaj razdelili na dve točki, ločeni glede na imenovalec.
Ulomka imata enak imenovalec
Če imata ulomka enak imenovalec ju odštejemo tako, da odštejemo samo njuna števca, imenovalec pa prepišemo. Torej velja:
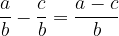
Ulomka imata različen imenovalec
Če imata ulomka različna imenovalca, ju moramo najprej razširiti na skupni imenovalec. Torej velja:
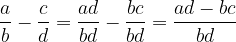
Ulomka zmnožimo tako, da zmnožimo oba števca med sabo in oba imenovalca med sabo. Torej:
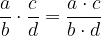
Za množenje ulomkov veljajo naslednji tri zakoni:
Komutativnost je zakon o zamenjavi. Torej množenje dveh ulomkov je komutativno kadar:
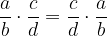
Asociativnost je zakon o združevanju. Množenje je asociativna operacija, torej velja:
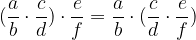
Seštevanje in množenje ulomkov povezuje zakon o distributivnosti oziroma zakon o razčlenjevanju:

Da lahko definiramo deljenje ulomkov si moramo najprej pojasniti kaj je to obratna vrednost ulomka.
Obratna vrednost ulomka 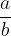 , pri čemer sta a in b neničeni, je ulomek
, pri čemer sta a in b neničeni, je ulomek  .
.
Formalno to zapišemo kot:
Obratno vrednost ulomka 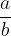 definiramo kot:
definiramo kot:
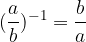
Produkt danega in njemu obratnega ulomka je enak 1. Torej velja:
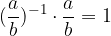
Sedaj lahko definiramo deljenje ulomkov kot:
Ulomek 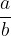 delimo z neničelnim ulomkom
delimo z neničelnim ulomkom 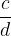 (c različen od 0) tako, da ulomek
(c različen od 0) tako, da ulomek 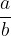 množimo z obratno vrednostjo ulomka
množimo z obratno vrednostjo ulomka 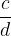 :
:
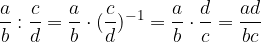
Opomba: Deljenje lahko tudi zapišemo v obliki dvojnega ulomka:
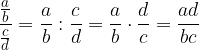
Ulomek razširimo tako, da števec in imenovalec pomnožimo z istim neničelnim številom. Dobljeni ulomek predstavlja isto racionalno število kot prvotni. Torej:
Ulomka 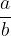 in
in 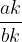 sta za neničelno število k enaka:
sta za neničelno število k enaka:
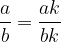
Ulomek krajšamo tako, da števec in imenovalec delimo s poljubnim skupnim deliteljem teh dveh števil. Dobljeni ulomek predstavlja isto racionalno število kot prvotni.
Ulomek je okrajšan, če sta števec in imenovalec tuji števili. Vsak ulomek je ekvivalenten natanko enemu okrajšanemu ulomku s pozitivnim imenovalcem. Da ulomek okrajšamo, moramo preprosto deliti števec in imenovalec z njunim največjim skupnim deliteljem.