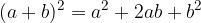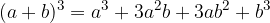S kompleksnimi števili računamo po pravilih za računanje z veččleniki, s tem da:
obravnavamo imaginarno enoto i kot vsako drugo algebraično količino in
upoštevamo vrednosti posameznih potenc imaginarne enote i
Pri računanju, zlasti pri množenju in potenciranju kompleksnih števil, dobimo potence imaginarne enote i, zato si bomo najprej ogledati kakšne so njihove vrednosti in šele potem računske operacije med kompleksnimi števili.
Potence imaginarne enote i
Pri potenciranju imaginarne enote upoštevamo, da za poljuben 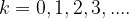 velja:
velja:
Vidimo, da moramo za izračun potence 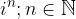 , število n deliti s štiri in da je z ostankom pri tem deljenju določena vrednost potence.
, število n deliti s štiri in da je z ostankom pri tem deljenju določena vrednost potence.
Poglejmo si konkreten primer izračuna potence imaginarne enote:
Primer
Primer je brezplačno dostopen prijavljenim uporabnikom.
Prijavi se za brezplačen dostop do primera »
Za brezplačen dostop do primera je potrebno izpolniti svoj profil.
Popolni svoj profil »
Seštevanje in odštevanje kompleksnih števil
Vsota oziroma razlika kompleksnih števil je kompleksno število, katerega realna komponenta je vsota oziroma razlika njihovih realnih komponent, imaginarna komponenta pa vsota oziroma razlika njihovih imaginarnih komponent.
Poglejmo si seštevanje oziroma odštevanje kompleksnih števil na konkretnem primeru:
Primer
Primer je brezplačno dostopen prijavljenim uporabnikom.
Prijavi se za brezplačen dostop do primera »
Za brezplačen dostop do primera je potrebno izpolniti svoj profil.
Popolni svoj profil »
Množenje kompleksnih števil
Kompleksna števila množimo po pravilih množenja veččlenikov.
Primer
Primer je brezplačno dostopen prijavljenim uporabnikom.
Prijavi se za brezplačen dostop do primera »
Za brezplačen dostop do primera je potrebno izpolniti svoj profil.
Popolni svoj profil »
Primer
Primer je brezplačno dostopen prijavljenim uporabnikom.
Prijavi se za brezplačen dostop do primera »
Za brezplačen dostop do primera je potrebno izpolniti svoj profil.
Popolni svoj profil »
Primer
Primer je brezplačno dostopen prijavljenim uporabnikom.
Prijavi se za brezplačen dostop do primera »
Za brezplačen dostop do primera je potrebno izpolniti svoj profil.
Popolni svoj profil »
Potenciranje kompleksnih števil
Kompleksna števila potenciramo s pomočjo obrazcev za kvadrat in kub dvočlenika:
s tem, da si pri višjih potencah pomagamo z ustreznim postopnim potenciranjem.
Primer
Primer je brezplačno dostopen prijavljenim uporabnikom.
Prijavi se za brezplačen dostop do primera »
Za brezplačen dostop do primera je potrebno izpolniti svoj profil.
Popolni svoj profil »
Primer
Primer je brezplačno dostopen prijavljenim uporabnikom.
Prijavi se za brezplačen dostop do primera »
Za brezplačen dostop do primera je potrebno izpolniti svoj profil.
Popolni svoj profil »
Seštevanje, odštevanje, množenje in potenciranje komleksnih števil
Za seštevanje, odštevanje, množenje in potenciranje kompleksnih števil veljajo običajna računska pravila seštevanja, odštevanja,množenja in potenciranja veččlenikov.
Poglejmo si primer, v katerem nastopajo različne računske operacije:
Primer
Primer je brezplačno dostopen prijavljenim uporabnikom.
Prijavi se za brezplačen dostop do primera »
Za brezplačen dostop do primera je potrebno izpolniti svoj profil.
Popolni svoj profil »
Enakost kompleksnih števil
Dve kompleksni števili sta enaki natanko takrat, ko sta enaki njuni realni komponenti in tudi imaginarni komponenti.
Poglejmo si konkreten primer uporabe definicije enakosti kompleksnih števil:
Primer
Primer je brezplačno dostopen prijavljenim uporabnikom.
Prijavi se za brezplačen dostop do primera »
Za brezplačen dostop do primera je potrebno izpolniti svoj profil.
Popolni svoj profil »


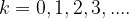 velja:
velja: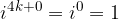
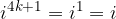
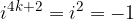
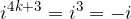
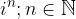 , število n deliti s štiri in da je z ostankom pri tem deljenju določena vrednost potence.
, število n deliti s štiri in da je z ostankom pri tem deljenju določena vrednost potence.