Osebne zbirke


V tem podpoglavju si bomo pogledali računske operacije med polinomi.
Polinome lahko:
seštevamo,
odštevamo,
množimo s številom,
množimo dva polinoma,
delimo.
Vse naštete operacije so notranje operacije. To pomeni, da je rezultat operacij vedno polinom. Poglejmo si jih.
Vsota dveh polinomov je vedno polinom.
Polinoma seštejemo tako, da seštejemo koeficienta pri potencah iste stopnje.
Stopnja vsote je enaka višji od stopenj obeh sumandov. Izjema se zgodi takrat, ko seštevamo polinoma iste stopnje, ki imata enaka a nasprotno predznačena koeficienta najvišjih stopenj. Najvišji stopnji se odštejeta in rezultat je polinom nižje stopnje.
Polinom pomnožen z neničelnim številom je ponovno polinom iste stopnje. Če polinom pomnožimo z 0, dobimo ničelni polinom.
Polinom pomnožimo s številom različnim od nič tako, da s tem številom pomnožimo vse njegove koeficiente.
Razlika dveh polinomov je vedno polinom.
Polinoma odštejemo tako, da odštejemo koeficienta pri potencah iste stopnje.
Stopnja razlike je enaka višji od stopenj obeh sumandov. Izjema se zgodi, ko odštevamo polinoma iste stopnje, ki imata za koeficienta najvišje stopnje enaki števili. Takrat je razlika polinomov nižje stopnje.
Produkt dveh polinomov je vedno polinom.
Polinoma zmnožimo tako, da vsak člen prvega polinoma pomnožimo z vsakim členom drugega polinoma. Gre torej za množenje veččlenikov.
Vodilni koeficient produkta polinomov je enak produktu vodilnih koeficientov obeh faktorjev. Posledično je stopnja produkta neničelnih polinomov je enaka vsoti stopenj polinomov, ki jih množimo.
Polinome lahko množimo s podpisovanjem. Ponovimo zgornji primer tako, da še enkrat zmnožimo s podpisovanjem.
Množenje polinomov s podpisovanjem je bolj pregleden način, če množimo polinoma, kjer je vsaj en polinom visoke stopnje, npr. 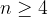 .
.
Deljenje dveh polinomov je težje od deljenja naravnih števil, a pri obeh se skriva podobna teorija. Pri naravnih številih gre za osnovni izrek o deljenju naravnih števil. Pri deljenju polinomov pa upoštevamo naslednje pravilo:
Polinom 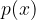 , stopnje m, nam da pri deljenju s polinomom
, stopnje m, nam da pri deljenju s polinomom 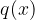 , stopnje n, da kvocient
, stopnje n, da kvocient 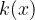 , stopnje m-n in ostanek
, stopnje m-n in ostanek 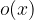 , če velja:
, če velja:
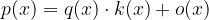
in je stopnja polinoma 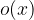 strogo manjša od stopnje delitelja
strogo manjša od stopnje delitelja 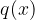 .
.
Torej, tako kot ne moremo v množici naravnih števil zdeliti 20 z 6 brez ostanka, saj je
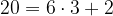
tako ne bomo mogli v splošnem brez ostanka zdeliti dveh poljubnih polinomov.
Obstajajo še drugi načini, kako lahko delimo polinome. Eden je Hornerjev algoritem, ki nam omogoči enostavno deljenje polinoma z linearnim polinomom.