Osebne zbirke


V poglavju o o grafu racionalne funkcije smo že spoznali racionalne funkcije in njihove lastnosti. Sedaj pa si bomo pogledali še v kakšnem razmerju sta lahko dve racionalni funkciji oz. dva grafa racionalnih funkcij.
Imejmo dve racionalni funkciji:
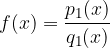
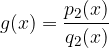
Ko obravnavamo dve racionalni funkciji, nas zanima:
presečišče funkcij; enačimo funkciji oziroma rešujemo racionalno enačbo.
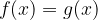
na katerih območjih so vrednosti prve funkcije večje (ali manjše) od vrednosti druge; problem rešujemo z neenačajem oziroma rešujemo racionalno neenačbo.
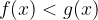
Naj bosta dani dve racionalni enačbi:
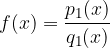
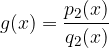
kjer so 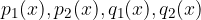 polinomi in
polinomi in 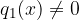 ,
, 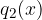 . Če želimo poiskati presečišče obeh racionalnih enačb, enačimo ordinati:
. Če želimo poiskati presečišče obeh racionalnih enačb, enačimo ordinati:
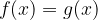
oziroma, če obe funkciji izpišemo:
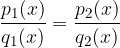
Takemu iskanju presečišč rečemo reševanje racionalne enačbe.
Iščemo torej ustrezne 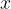 , za katere velja zgornja enakost. To storimo tako, da enačbo preoblikujemo:
, za katere velja zgornja enakost. To storimo tako, da enačbo preoblikujemo:
Ulomek ima vrednost 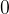 , kadar je števec enak
, kadar je števec enak 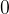 , imenovalec pa različen od
, imenovalec pa različen od 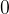 .
.
Iščemo torej rešitve enačbe:
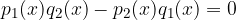
Pri iskanju rešitev pa moramo paziti, da rešitve ne sovpadejo z rešitvami enačbe:
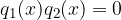
Rešitve slednje enačbe so nedovoljene oziroma prepovedane rešitve in jih v končni rešitvi ne smemo upoštevati.
Naj bosta dani dve racionalni funkciji,
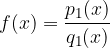
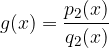
kjer so 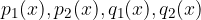 polinomi in
polinomi in 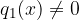 ,
, 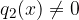 .
.
Ko iščemo vrednost 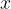 , za katere je racionalna funkcija
, za katere je racionalna funkcija 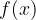 pod racionalno funkcijo
pod racionalno funkcijo 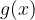 (vrednosti ordinate racionalne funkcije
(vrednosti ordinate racionalne funkcije 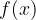 so manjše od vrednosti racionalne funkcije
so manjše od vrednosti racionalne funkcije 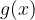 ), rešujemo racionalno neenačbo:
), rešujemo racionalno neenačbo:
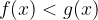
Oziroma, če obe funkciji izpišemo:
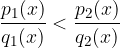
Takemu iskanju ustreznih rešitev rečemo reševanje racionalne neenačbe. Iščemo torej ustrezne 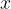 , za katere velja zgornja neenakost.
, za katere velja zgornja neenakost.
Neenačbo preoblikujemo:
Da bomo dosegli zgornjo neenakost (da bo vrednost na levi strani manjša od 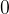 ) mora biti eden izmed števca in imenovalca manjši od
) mora biti eden izmed števca in imenovalca manjši od 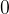 , drugi pa večji od
, drugi pa večji od 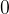 . Poleg tega mora biti imenovalec obvezno različen od
. Poleg tega mora biti imenovalec obvezno različen od 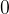 .
.
Velja ena izmed dveh možnosti. Prva možnost je:
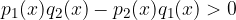
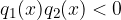
druga možnost je:
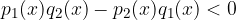
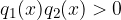
Na povsem enak način, kot smo iskali rešitev za:
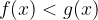
lahko iščemo rešitve še za naslednje neenačbe:
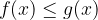
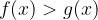
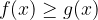
Poglejmo si vse kombinacije in njihove rešitve:
Neenačbe lahko rešujemo računsko ali grafično. Poglejmo si primer.