Prijava z e-naslovom
Prijava brez gesla
Pojem razdalja vedno pomeni razdaljo med dvema točkama. To pa si lahko predstavljamo kot dolžino daljice, ki ima ti dve točki za krajišči.
Tudi kadar računamo razdaljo med :
točko T in premico p,
točko T in ravnino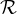 
,
zares računamo razdaljo med točko T in ustrezno točko na premici oziroma ravnini.
V tem gradivu bomo spoznali, kako računamo razdaljo med geometrijskimi elementi, ki imajo poljubno lego v prostoru.
Na spodnji sliki točka A leži na ravnini 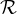, točka B pa izven ravnine 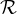. Razdaljo med točkama A in B predstavlja dolžina daljice AB.
Razdalja med točkama v prostoru
Razdaljo med točkama A in B označimo z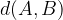 
. Krajše pa jo zapišemo kot označimo z 
.
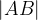Razdaljo med točkama A in B označimo z :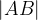
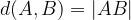
Če razdalje med točkama ne poznamo, si lahko pri računanju razdalje pomagamo tako, da si v prostoru predstavljamo pravokotni trikotnik:
kateti predstavljata dve znani razdalji,
neznano razdaljo pa izračunamo z uporabo Pitagorovega izreka.
Na spodnji sliki imamo tri točke:
točki A in T ležita na ravnini ,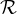
točka B pa izven ravnine.
Vse tri točke tvorijo pravokotni trikotnik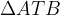 
:
Pravokotni trikotnik v prostoru
Razdalja med točko in premico predstavlja najkrajšo razdaljo med njima. To je dolžina tiste daljice, ki je pravokotna na premico.
Na spodnji sliki točka P leži na ravnini 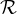, točka T pa izven ravnine :
Razdalja med točko in premico
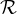Razdaljo med točko in premico je smiselno računati, če točka ne leži na premici. Če točka leži na premici, je razdalja med točko in premico enaka 0.
Razdalja med točko T in premico p je dolžina daljice TP, ki je pravokotna na premico p. Točka P pri tem leži na premici p.
Z matematičnimi simboli razdaljo med točko T in premico p zapišemo na naslednji način: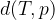 
Velja tudi enakost: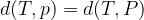 
Razdalja med točko in ravnino predstavlja najkrajšo razdaljo med njima. To je dolžina tiste daljice, ki je pravokotna na ravnino.
Na spodnji sliki točka R leži na ravnini 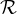, točka T pa izven ravnine, točno nad točko R:
Razdalja med točko in ravnino
Razdaljo med točko in ravnino je smiselno računati, če točka ne leži na ravnini, saj je v nasprotnem primeru ta enaka 0.
Razdalja med poljubno točko T in ravnino 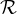je razdalja daljice TR, ki je pravokotna na ravnino 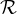. Točka R pri tem leži na ravnini .
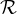Z matematičnimi simboli razdaljo med točko T in ravnino 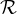zapišemo na naslednji način: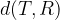 
Velja tudi enakost: 
