Osebne zbirke


Razmerje je primerjava količin po velikosti. Pove nam, kolikokrat je ena količina večja od druge.
Zadeve si lahko poenostavimo, če razmerje izrazimo v matematični obliki. Če želimo primerjati količini a in b, to z razmerjem zapišemo:
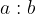
K zapisu razmerja dodamo še številske vrednosti količin.
Naj bosta a in b velikosti dveh količin. V matematiki dve količini praviloma primerjamo tako, da zapišemo njun količnik v obliki deljenja ali pa ulomka:

Ta količnik imenujemo razmerje in ga beremo a proti b. Število a je prvi člen razmerja, število b je drugi člen razmerja.
V razmerju moramo obe količini izraziti z enakima merskima enotama.
Za skupno mersko enoto izberemo manjšo mersko enoto. Razmerje potem zapišemo samo s številoma, brez merskih enot.
Razmerje količin a in b lahko zapišemo kot ulomek 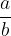 , zato za razmerja veljajo enake lastnosti kot za ulomke.
, zato za razmerja veljajo enake lastnosti kot za ulomke.
To pomeni, da moramo tudi razmerje poenostaviti, če je mogoče. Poenostavimo ga tako, da ga:
razširjamo
ali krajšamo.
Razmerje je poenostavljeno, ko sta števili a in b:
naravni števili
in tuji števili
Takrat je največji skupni delitelj števil a in b enak 1.
Poenostavljeno razmerje je povsem enako prvotnemu razmerju - le drugače je zapisano. To bomo videli v nadaljevnaju pri računanju količnika razmerja. Poglejmo si podrobneje, na kakšne načine lahko poenostavimo razmerje.
Razmerje razširimo zato, da oba člena razmerja a in b pretvorimo v naravni števili.
Z razširjanjem v razmerju odpravljamo:
decimalna števila
ali ulomke.
Razmerje razširimo tako, da oba člena pomnožimo z enakim, od nič različnim številom.
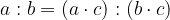
Decimalna ševila v razmerju odpravimo tako, da razmerje pomnožimo z večkratnikom števila 10. S katerim, je odvisno od najnatančnejšega decimalnega mesta v razmerju:
z 10, če je najnatančneje decimalno mesto v razmerju desetina,
s 100, če je najnatančneje decimalno mesto v razmerju stotina,
s 1000, če je najnatančneje decimalno mesto v razmerju tisočina,
in tako dalje.
Ulomke v razmerju odpravimo tako, da razmerje pomnožimo z najmanjšim skupnim imenovalcem.
Zaporedje krajšamo z namenom, da dobimo poenostavljeno razmerje, v katerem sta člena zaporedja tuji naravni števili (njun največji skupni delitelj je enak 1).
Razmerje krajšamo tako, da oba člena delimo z enakim, od nič različnim številom.
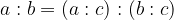
Če v razmerju nakazano deljenje tudi izračunamo, dobimo količnik razmerja, ki ga označimo s k.
Količnik razmerja k nam pove, da je prvi člen k-krat večji od drugega člena razmerja.
Takrat lako razmerje zapišemo v obliki:
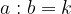
Poglejmo si količnik razmerja v primeru.
Poglejmo si še, kako ugotovimo, če sta dve razmerji enaki.
Lastnost razmerja je njegov količnik k. Če imata dve razmerji enak količnik, npr. 3, potem nam obe razmerji povesta isto stvar - da je prva količina 3-krat večja od druge. Taki razmerji sta torej enaki.
Dve razmerji sta enaki, kadar imata enak količnik razmerja k.
Sorazmerje označuje enakost dveh razmerij. Uporabimo ga za izračun neznane količine, če poznamo v kakšnem razmerju je z neko znano količino. Poglejmo si sorazmerje na konkretnem primeru.
Kaj pa, če je primer zapletenjši? Potem moramo neznano količino izračunati.
Najprej si pogljemo, kako zapišemo sorazmerje. Če sta dve razmerji enaki, potem imata enak količnik k.
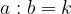
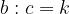
Takrat lahko zapišemo:
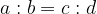
Dobili smo enačbo, ki jo imenujemo sorazmerje in jo beremo a proti b je kakor c proti d. Zdaj vidimo, zakaj je sorazmerje isto kot enakost dveh razmerij.
Števili a in d imenujemo zunanja člena, b in c pa notranja člena sorazmerja.
Zapis 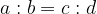 pomeni enakost ulomkov, zato lahko zapišemo:
pomeni enakost ulomkov, zato lahko zapišemo:
S tem preprostim računom smo prišli do pomembnega pravila:
V poljubnem sorazmerju je produkt zunanjih členov enak produktu notranjih členov.
To pravilo uporabimo takrat, ko je eden od členov sorazmerja neznan in ga moramo izračunati.
Pri poenostavljanju (natančneje pri razširjanju) razmerja smo spoznali, da se razmerje ne spremeni, če oba člena množimo z istim, od nič različnim številom.
Količini a in b, ki sta v razmerju, lahko zapišemo kot:
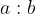
Če razmerje razširimo s poljubnim, od nič različnim številom x, dobimo povsem enako razmerje:
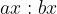
Gornji zapis lahko razumemo, da smo oba člena razmerja zapisali z neko enoto x. Pri tem pa ima:
prvi člen: število takih enot enako 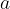 ,
,
drugi člen: število takih enot enako 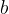 .
.
V zgornjem primeru smo videli, kako lahko podano razmerje uporabimo za zapis podatkov v nalogi. Tak zapis količin nam omogoča reševanje besedilnih nalog, v katerih je podano razmerje.
Poglejmo si primer take naloge.