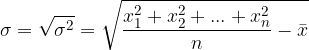Osebne zbirke


V poglavju srednje vrednosti smo spoznali več poti za računanje srednje vrednosti oz. tipičnega podatka, ki lahko predstavlja določeno množico podatkov. A srednja vrednost v splošnem preslabo opiše množico podatkov - če več, lahko nas napelje na zmoten sklep. Za ilustracijo takega primera si poglejmo naslednji zgled.
Da bi lahko informacijo o povprečni vrednosti bolje razumeli (in ne bili zavedeni), vpeljemo novo mero, ki ji rečemo razpršenost podatkov. Razpršenost podatkov si lahko predstavljamo kot vrednost, ki nam pove, kako blizu so podatki povprečni vrednosti:
tem manjša je razpršenost, tem bolje odraža povprečna vrednost tipično vrednost naključnega podatka;
tem večja je razpršenost, tem slabše odraža povprečna vrednost tipično vrednost naključnega podatka.
Razpršenosti podatkov je informacija o tem, kako so podatki porazdeljeni.
Razpršenost podatkov lahko izračunamo na več načinov, vendar bomo v tem gradivu spoznali le nekatere najpomembnejše. To so:
variacijski razmik,
varianca,
standardni odklon.
Poglejmo si natančneje vsakega posebej.
Najpreprosteje ga določimo tako, poiščemo največjo in najmanjšo vrednost med podatki ter ju odštejemo. Zapišimo:
Variacijski razmik je razlika med maksimalno in minimalno vrednostjo podatka. Označimo ga z R:
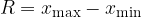
Variacijski razmik je zelo odvisen od ekstremnih vrednosti, posebno osamelcev, zato ga uporabljamo le v kombinaciji z drugimi merami razpršenosti.
Varianca je najpomembnejša mera za razpršenost podatkov. Pokaže nam stopnjo odstopanja podatkov od povprečja (aritmetične sredine).
Do variance pa pridemo z naslednim razmislekom: če bi sešteli vsa odstopanja od aritmetične sredine - vrednosti večje od povprečja imajo pozitivno odstopanje, vrednosti manjše od povprečja pa negativno - bi se odstopanja seštela natanko v nič. Da se vrednosti ne bi seštele v nič, se znebimo negativnih vrednosti tako, da odstopanja kvadriramo in jih seštejemo.
Varianca predstavlja povprečje kvadratov odmikov podatkov od srednje vrednosti. Izračunamo jo kot:
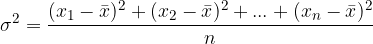
S preoblikovanje enačbe (dokaz izpustimo) lahko varianco izračunamo tudi kot:
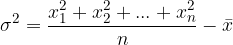
Kot rečeno: varianca je mera za razpršenost podatkov. Večja kot je varianca, bolj so podatki razpršeni. A varianca nam podaja mero v kvadrirani obliki. Želimo podatek, ki bo primerljiv s povprečno vrednostjo, zato varianco korenimo; korenjeno varianco imenujemo standardni odklon.
S standardnim odklonom izmerimo kako razpršene so vrednosti, vsebovane v populaciji. Izračunamo ga kot:
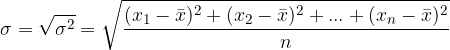
oziroma kot: