Prijava z e-naslovom
Prijava brez gesla
V tem gradivu si bomo ogledali reševanje enačb in neenačb.
Enačbo si lahko predstavljamo kot tehtnico. Ta je v ravnovesju, ko je masa na levi strani enaka masi na desni.
Rešiti enačbo torej pomeni ugotoviti, kakšna mora biti vrednost neznanke (na primer 
), a da bo enačba uravnotežena. Z drugimi besedami: da bo vrednost na levi strani enačaja enaka vrednosti na desni strani.
Do rešitve enačbe lahko pridemo na več načinov. Pri lažjih enačbah nam pomaga že logičen razmislek, za zapletenejše enačbe pa si lahko pomagamo s prenašanjem členov ali z uporabo računskih operacij nad enačbami.
Najprej si oglejmo, kako s pomočjo logičnega sklepanja in prenašanja členov rešujemo enačbe.
Cilj vsakega reševanja enačbe je ugotoviti vrednost neznanke. To naredimo tako, da preuredimo enačbo in člen z neznanko pustimo samega na eni strani enačbe, medtem ko vse druge člene prenesemo na drugo stran.
Če neznanka stoji sama zase, lahko do rešitve pridemo z enostavnimi matematičnimi operacijami, kot sta seštevanje ali odštevanje.
Tej poenostavitvi, ki smo jo spoznali v gornjem primeru, bomo rekli Reševanje enačb s prenašanjem števil. Enačbe bomo reševali tako, kot da lahko števila prenašamo iz ene strani na drugo. S tem dosežemo, da na eni strani enačbe ostane samo in ga tako lahko izračunamo.
Na številu ki ga "prenesemo" čez enačaj, na drugi strani enačbe uporabimo obratno operacijo.
Prištevanje števila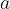 
na eni strani enačbe tako postane postane odštevanje števila 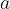na drugi strani enačbe.
Rešimo še en primer. Upoštevajmo gornjo poenostavitev in prenašamo števila čez enačaj.
Če člen z neznanko vsebuje še kakšen koeficient, je potrebno za rešitev enačbe uporabiti tudi množenje ali deljenje. Postopka bomo spoznali v nadaljevanju.
Poglejmo enačbo, v kateri ob neznanki nastopa množenje.
Množenje s številom 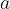na eni strani enačbe postane deljenje s številom 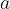na drugi strani enačbe.
Rešimo še en primer:
Poglejmo še enačbo, v kateri člen z neznanko vsebuje ulomek, neznanka pa se nahaja v števcu ulomka.
Spomnimo se, da ulomkova črta pomeni računsko operacijo deljenja.
Deljenje s številom 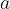na eni strani enačbe postane množenje s številom 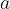na drugi strani enačbe.
Rešimo še en primer:
Enačbe, ki vključujejo več različnih računskih operacij hkrati, imajo običajno več členov, člen z neznanko pa pogosto vsebuje še kakšen dodatni koeficient.
Pri reševanju takih enačb je potrebno upoštevati vrstni red računanja, ki je ravno nasproten od vrstnega reda računanja izrazov. Najprej prenašamo člene preko enačaja, na koncu pa množimo in delimo.
S prenašanjem členov čez enačaj najprej osamimo člen, v katerem nahaja neznanka, nato pa odpravimo še koeficiente v členu z neznanko. Pri tem ves čas pazimo, da ohranjamo ravnovesje enačbe. Na koncu neznanka ostane sama na svoji strani enačaja.
Enačbe z mešanimi operacijami rešujemo tako da:
najprej prestavimo člene, ki ne vsebujejo neznanke, na svojo stran enačbe
po potrebi množimo ali delimo, da odpravimo koeficiente, ki se nahajajo v istem členu kot neznanka.
Tudi neenačbo si lahko predstavljamo kot tehtnico. Ampak ta tehtnica običajno ni v ravnovesju, tako da je masa na levi strani večja ali manjša od mase na desni. Le v posebnih primerih se zgodi, da sta masi enaki.
Neznanka (na primer ) ima zato lahko več vrednosti, saj je enačba lahko bolj ali manj "nagnjena" iz ravnotežja.
Če neznanko postavimo na levo stran neenačbe, znano vrednost 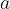pa na desno stran, lahko sestavimo štiri kombinacije z znakom neenakosti:
neznanka je (strogo) manjša od znane vrednosti, kar zapišemo kot:
neznanka je manjša ali enaka znani vrednosti, kar zapišemo kot:
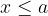
neznanka je (strogo) večja od znane vrednosti, kar zapišemo kot:
neznanka je večja ali enaka znani vrednosti, kar zapišemo kot:
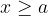
Tudi neenačbe bomo reševali s prenašanjem členov:
Tudi pri neenačbah želimo imeti na eni strani, ostala števila pa na drugi strani. To dosežemo s prenašanjem števil z ene strani na drugo.
Na številu ki ga "prenesemo" čez neenačaj, na drugi strani enačbe uporabimo obratno operacijo.
Prištevanje števila 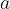na eni strani neenačbe tako postane postane odštevanje števila 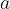na drugi strani neenačbe.
Rešimo naslednji primer s prenašanjem števila čez enačaj.
Iz enačb vemo, da množenje z leve strani postane deljenje na desni strani.
Množenje s številom 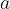na eni strani neenačbe postane deljenje s številom 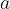na drugi strani neenačbe.
Postopek si oglejmo na naslednjem primeru.
Prav tako vemo, da deljenje z leve strani postane množenje na desni strani.
Deljenje s številom 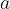na eni strani neenačbe postane množenje s številom 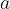na drugi strani neenačbe.
Postopek si oglejmo na naslednjem primeru.
Tudi pri reševanju zahtevnejših neenačb je potrebno upoštevati vrstni red računanja, ki je nasproten od vrstnega reda računanja izrazov. Najprej prenašamo člene preko neenačaja, na koncu pa množimo in delimo.
S prenašanjem členov čez neenačaj najprej osamimo člen, v katerem nahaja neznanka, nato pa odpravimo še koeficiente v členu z neznanko. Na koncu neznanka ostane sama na svoji strani neenačaja.
