Osebne zbirke


Linearno enačbo dobimo kadar z enačajem povežemo dva linearna izraza, v katerih nastopa neznana količina na prvo potenco. Neznano količino ponavadi označimo z x.
Linearna enačba je v matematiki enačba, v kateri je vsak člen ali konstanta ali produkt konstant s prvo potenco neznanke. Simbolno jo zapišemo kot:
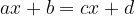
pri čemer so 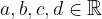
Reševanje problemov iz vsakdanjega življenja zahteva od nas nekoliko več napora, saj jih moramo najprej prevesti v matematično jezik. Kadar enačbe rešujemo, to pomeni, da iščemo vse take vrednosti neznanke x, za katere je izraz resničen. Pri tem sledimo spodnjim točkam:
Razumevanje problema
Najprej moramo problem razumeti. Razumeti moramo kaj je neznanka in kaj konstanta, kateri podatki so na voljo, kakšni so pogoji in na kaj moramo biti pozorni.
Napišemo enačbo
Poiščemo zvezo med podatki in neznanko. Pri tem nam je lahko v pomoč, če se spomnimo podobnih problemov, ki smo jih že reševali.
Rešimo enačbo ali sistem enačb
Iz enačbe izrazimo neznanke. Naš cilj je zapisati neznanke s pomočjo čim manj ostalih neznank (če je možno tudi z nič neznankami). Ponavadi je reševanje enačb oziroma sistemov enačb dolg postopek, zato je pomembno, da dobro preverimo vsak korak reševanja.
Preverimo dobljeno rešitev
Rešitev vstavimo v prvotno enačbo. Včasih že z logičnim premislekom lahko ugotovimo, ali je rešitev pravilna ali protislovna. Pri mnogih nalogah rezultat lahko ocenimo na pamet. Računsko preverimo tako, da vstavimo rešitev v enačbo in na koncu se mora enakost ujemati. Kadar je rezultat mogoče izračunati na več načinov, se morajo rezultati med seboj ujemati.
Za lažje razumevanje zgornje točke pokažimo na realnem primeru:
Pri reševanju enačb pa naletimo včasih tudi na probleme. Oglejmo si dva primera:
Za lažje razumevanje si poglejmo naslednji primer:
S pomočjo zgornjega izračuna opazimo, da enakost velja, vendar nimamo izražene neznanke x. Taki enačbi pravimo identična enačba, njena rešitev pa je katerokoli realno število.
Tudi tukaj si za lažje razumevanje poglejmo naslednji primer:
S pomočjo zgornjega izračuna ugotovimo, da se neznanke izničijo in dobimo enakost, ki ne more veljati pri nobenem realnem številu, zato ta enačba nima rešitve.
Če v linearni enačbi na obeh straneh prištejemo ali odštejemo isto število ali obe strani pomnožimo ali delimo z istim od nič različnim številom, dobimo enakovredno (ekvivalentno) enačbo, to pomeni enačbo, ki ima iste rešitve kot prvotna enačba.
Z dosedanjim znanjem bomo znali rešiti tudi nekatere kvadratne enačbe ali enačbe višjih stopenj. To so enačbe, v katerih neznanka nastopa z drugo ali celo višjo potenco. Takih enačb se lotimo na naslednji način:
Preoblikovnje enačbe
Z osnovnimi operacijami preoblikujemo enačbo v enakovredno enačbo, ki ima vse člene na levi strani, na desni strani pa ostane samo nič.
Združimo enakovredne člene
...kar pomeni, da enačbo (člene, ki se nahajajo vsi na isti strani) poračunamo.
Razcepimo izraz na linearne člene
Poračunano levo stran (če se da) razcepimo na same linearne faktorje.
Obravnava posameznih členov
Vsakega izmed razcepljenih (v najboljšem primeru linearnih) členov enačimo z nič. Namreč, vemo, da je produkt (linearnih) faktorjev enak 0 samo v primeru, če je vsaj eden od faktorjev enak 0:
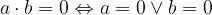
Po zgornjem postopku kvadratno enačbo prevedemo na dve linearni enačbi, enačbo tretje stopnje prevedemo na tri linearne enačbe itd. Enačba ima toliko rešitev kot je njena stopnja. Takšni enačbi rečemo razcepna enačba.
Najprej si poglejmo obliko sistema dveh linearnih enačb:
Sistem dveh linearnih enačb z dvema neznankama x in y je oblike:
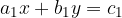
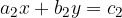
pri čemer so 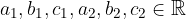
Rešiti sistem dveh linearnih enačb pomeni poiskati taki vrednosti za neznanki x in y, da bosta zadoščali obema enačbama sistema. Sistem enačb lahko rešimo na več načinov, v nadaljevanju si bomo ogledali dva.
Sistem dveh enačb z dvema neznankama rešujemo na zamenjalni način tako, da iz poljubno izbrane enačbe izrazimo eno neznanko. Nato izraženo vstavimo namesto te neznanke v preostalo enačbo.
Tako se znebimo izražene neznanke. Dobimo eno enačbo z eno neznanko, ki je ni težko rešiti. Nato le še izračunamo manjkajočo neznanko.
Princip za reševanje sistema dveh enačb z dvema neznankama s pomočjo metode nasprotnih koeficientov je naslednji:
Eno ali obe enačbi pomnožimo tako, da dobimo pred isto neznanko v obeh enačbah nasprotna koeficienta.
Enačbi nato seštejemo in s tem izločimo eno neznanko.
Izračunamo še vrednost izločene neznanke.
Opomba: Kadar rešujemo probleme iz vsakdanjega življenja, jih moramo najprej prevesti v matematični jezik, potem pa pride na vrsto reševanje sistemov enačb.
V problemu lahko nastopa tudi več neznank. Če iščemo vrednost za tri neznanke, potrebujemo tri enačbe. Najprej si poglejmo obliko sistema treh linearnih enačb:
Sistem dveh linearnih enačb z dvema neznankama x in y je oblike:
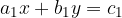
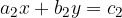
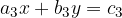
pri čemer so 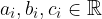 in
in 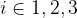
Take sisteme rešujemo podobno kot sisteme dveh enačb z dvema neznankama. Zamenjalni način je povsem enak, le da v tem primeru izraženo neznanko vstavimo v enačbo, kjer ponovno izrazimo neznanko, katero vstavimo v prvotno enačbo. Podrobneje si poglejmo metodo nasprotnih koeficientov.
Kot že vemo moramo enačbe množiti z določenimi števili in jih med seboj seštevati tako, da "odpade" katera od neznank. Zaradi boljše preglednosti pišemo števila pred neznanko (koeficiente) v matrike (vrstni red enačb lahko zamenjamo). Matrika je v splošnem naslednje oblike: