Osebne zbirke


Linearna neenačba je zapis sestavljen iz dveh linearnih matematičnih izrazov, ki ju imenujemo leva in desna stran neenačbe. Povezuje ju neenačaj, ki je lahko eden od naslednjih znakov:
 , ki pomeni strogo manjše
, ki pomeni strogo manjše
 , ki pomeni manjše ali enako
, ki pomeni manjše ali enako
 , ki pomeni strogo večje
, ki pomeni strogo večje
 , ki pomeni večje ali enako
, ki pomeni večje ali enako
V neenačbi nastopajo tudi spremenljivke, ki jih v tem primeru imenujemo neznanke. Najpogosteje neznanko označimo s črko x.
V splošnem je linearna neenačba naslednje oblike:
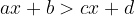
kjer so a, b, c, d konkretna števila.
Neenačbo rešimo tako, da spreminjamo dano neenačbo v enakovredno (ekvivalentno) neenačbo. To pomeni, da ima isto množico rešitev vendar je po obliki preprostejša.
Pri reševanju neenačb uporabljamo naslednje postopke, ki so posledica lastnosti relacije urejenosti realnih števil:
levi in desni strani neenačbe lahko prištejemo isto število (oz. neznanko ali daljši matematični izraz)
levo in desno stran neenačbe lahko pomnožimo ali delimo z istim pozitivnim številom (oz. neznanko ali daljši matematični izraz)
levo in desno stran neenačbe lahko pomnožimo ali delimo z istim negativnim številom, vendar se v tem primeru neenačaj v neenačbi obrne
Linearno neenačbo z eno neznanko (imenovano tudi neenačbo prve stopnje) rešimo tako, da prenesemo člene z neznanko na eno stran, člene brez neznanke pa na drugo stran.
Opomba: Po uporabi katerega od zgornjih postopkih, še vedno dobimo neenačbo enakovredno prvotni.
Za rešitev linearne neenačbe z eno neznanko velja natanko ena izmed naslednjih trditev:
Rešitev neenačbe je realno število, za katerega neenakost velja - torej, če vstavimo to število namesto neznanke, dobimo pravilen zapis. Množica rešitev linearne neenačbe je interval, ki je vsaj na eno stran ni omejen.