Osebne zbirke


Reševanje neenačb višje stopnje poteka podobno kot reševanje linearnih neenačb, le da so v neenačbi polinomi višjih stopenj. Splošna oblika neenačbe višje stopnje je:
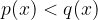
Navadno neenačbo najprej preoblikujemo v:
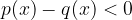
Neenačbo poenostavimo tako, da:
seštejmo ali odštejemo isto število ali matematični izraz na obeh straneh neenačbe
obe strani neenačbe pomnožimo ali delimo z istim pozitivnim številom
neenačbo delimo ali množimo z istim negativnim številom, pri tem obnemo neenačaj.
Preoblikovano neenačbo razstavimo na linearne faktorje, nato preučimo vsak faktor posebej. Pri razstavljanju polinomov na faktorje lahko uporabimo Hornerjev algoritem.
Pri reševanju neenačb višje stopnje je rešitev interval ali unija intervalov, ki ustrezajo iskanemu predpisu.
Ničle polinomov, ki jih dobimo iz linearnih faktorjev, predstavljajo mejo intervalov, na katerih pride do sprememb v predznaku. Ko dobimo mejnike, preverimo obnašanje polinoma na danem intervalu. Opomba: spomnimo se, da polinom zamenja predznak v lihih ničlah.
Šele ko imamo vse te podatke pogledamo, na katerem intervalu naša neenačba ustreza začetnemu predpisu.