Prijava z e-naslovom
Prijava brez gesla
Množica realnih števil je množica vseh neskončnih decimalnih števil.
Neskončna decimalna števila so števila, katerih decimalnih zapis ima neskončno decimalk. Pri tem je pomembno omeniti, da mednje štejemo tudi števila, katerih zapis je končen (saj lahko na koncu dodamo neskončno ničel).
Množica realnih števil se deli na naslednji množici:
množica racionalnih števil
množica iracionalnih števil.
Za začetek si na kratko poglejmo o katerih množicah sploh govorimo:
Racionalna števila so števila, ki jih lahko zapišemo z ulomki. Množico racionalnih števil označimo z: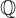 
Iracionalno število je po definiciji vsako realno število, ki ga ni mogoče zapisati v obliki ulomka. Torej iracionalna števila so vsi kvadratni koreni naravnih števil, katerih korenjenci niso popolni kvadrati, vsi kubični koreni celih števil, katerih korenjenci niso popolni kubi, itd.
Iracionalnih števil je neskončno mnogo. Če bi jih poskušali zapisati v decimalni obliki, bi dobili neskončno zaporedje neperidodičnih decimalk. Velja:
Med poljubnima dvema racionalnima številoma obstaja neskončno mnogo racionalnih števil in neskončno mnogo iracionalnih števil.
Od tukaj lahko vpeljemo množico realnih števil:
Če množico racionalnih števil razširimo tako, da so v njej zajeta tudi iracionalna števila, dobimi novo množico, ki jo imenujemo množica realnih števil.
Velja, da vsakemu realnemu številu pripada ena točka na številski premici in obratno, vsaka točka na številski premici je predstavnik enega realnega števila.
Za številske množice velja naslednja hierarhija :
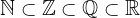
pri čemer je:
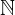... množica naravnih števil
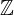... množica celih števil
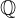... množica racionalnih števil
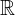... množica realnih števil
Za lažje razumevanje lahko to predstavimo s pomočjo naslednje skice:
V nadaljevanju si bomo pogledali računske operacije, ki jih lahko izvajamo nad množico realnih števil:
V množici realnih števil so definirane naslednje računske operacije:
seštevanje,
odštevanje,
množenje,
deljenje
za katere veljajo naslednje lastnosti:
Za poljubna realna števila a, b in c velja:
komutativnost seštevanja:
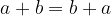
asociativnost seštevanja:
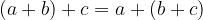
0 je enota za seštevanje:
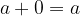
obstoj nasprotnega števila:
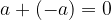
komutativnost množenja:
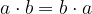
asociativnost množenja::
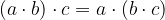
1 je enota za množenje:
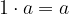
distributivnost:
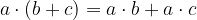
obstoj inverznega števila:
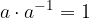
Posebej si poglejmo deljenje realnih števil:
Deljenje realnih števil lahko definiramo na naslednji način:
Naj bosta a in c poljubni realni števili in naj bo b poljubno neničelno realno število, tedaj lahko deljenje zapišemo kot:
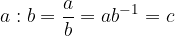
Od tukaj lahko vpeljemo ekvivalentno zvezo med množenjem in deljenjem:
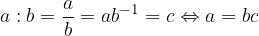
Za deljenje realnih števil veljajo naslednje lastnosti:
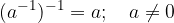
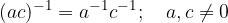
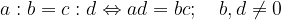
Množico realnih števil lahko zapišemo kot unijo treh paroma disjunktnih podmnožic:
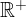... množica vseh pozitivnih realnih števil
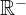... množica vseh negativnih realnih števil
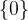... množica, ki vsebuje število nič
Simbolno to zapišemo kot:
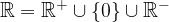
Kot vsa ostala števila si tudi realna števila najlažje predstavljamo na številski premici:
Za začetek zgoraj zapisano ponazorimo grafično:
Točka na številski premici predstavlja:
pozitivno realno število a (a>0) natanko takrat, ko leži desno od 0
negativno realno število a (a<0) natanko takrat, ko leži levo od 0
Kot vsa do sedaj poznana števila, lahko tudi realna števila urejamo po velikosti:
Množica realnih števil je urejena. Za poljubni realni števili a in b velja natanko ena od naslednjih trditev
Število a je večje od števila b (oznaka: 
) natanko takrat, ko je 
pozitivno število:
Na številski premici je točka, ki predstavlja število a desno od točke, ki predstavlja število b.
Grafična predstavitev:
Število a je manjše od števila b (oznaka: 
) natanko takrat, ko je 
negativno število:
Na številski premici je točka, ki predstavlja število a levo od točke, ki predstavlja število b.
Grafična predstavitev:
Število a je enako številu b (oznaka: 
) natanko takrat, ko je enako nič:
Na številski premici je točka, ki predstavlja število a na enakem mestu kot točka, ki predstavlja število b.
Grafična predstavitev:
Na množici realnih števil lahko definiramo lahko še naslednji relaciji urejenosti:
Število a je večje ali enako številu b (oznaka: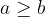 
) natanko takrat, ko je 
nenegativno število:
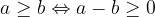
Na številski premici je točka, ki predstavlja število a na enakem mestu ali desno od točke , ki predstavlja število b.
Število a je manjše ali enako številu b (oznaka: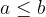 
) natanko takrat, ko je nepozitivno število:
Na številski premici je točka, ki predstavlja število a na enakem mestu ali levo od točke , ki predstavlja število b.
Zgornji trditvi lahko združimo v naslednjo ekvivalentno zvezo (zakon asimetričnosti):
Naj bosta a in b poljubni realni števili. Naj bo a večji ali enak od b in naj bo a manjši ali enak od b, potem velja, da je a enak b:
Simbolni zapis:
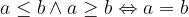
V nadaljevanju si bomo pogledali lastnosti zgoraj omenjenih relacij urejenosti:
Naj bodo a, b in c poljubna realna števila. Za njih veljajo naslednje lastnosti:
če je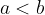 
potem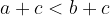 
Če na obeh straneh neenakosti prištejemo isto število, se neenakost ohrani (monotonost vsote).
če velja 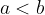in 
, potem 
Relacija "biti manjši" je tranzitivna.
če velja 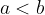in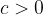 
, potem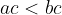 
Pri množenju neenakosti s pozitivnim številom se znak neenakosti ohranja.
če velja 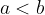in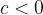
, potem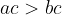 
Pri množenju neenakoti z negativnim številom se znak neenakosti obrne.
Opomba: Za računanje z enačbami in neenačbami veljajo vsa pravila, ki so opisana pri racionalnih številih.
