Osebne zbirke


Deljivost je relacija med števili. Naj bosta 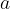 in
in 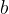 naravni števili. Rečemo, da število
naravni števili. Rečemo, da število 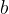 deli število
deli število 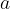 , če obstaja tako naravno število
, če obstaja tako naravno število 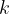 , da velja
, da velja
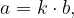
oziroma, 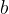 deli število
deli število 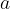 , če je
, če je 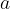 večkratnik števila
večkratnik števila 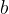 .
.
Zgornjo enakost 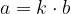 lahko preoblikujemo tudi v nam bolj znano obliko:
lahko preoblikujemo tudi v nam bolj znano obliko:
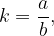
kjer
število 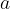 imenujemo deljenec
imenujemo deljenec
število 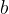 imenujemo delitelj
imenujemo delitelj
število 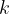 imenujemo količnik ali kvocient.
imenujemo količnik ali kvocient.
Relacijo deljivosti med številoma označimo z
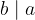
kar preberemo: b deli a.
Večkratnikov kateregakoli naravnega števila je neskončno, deliteljev pa končno mnogo.
Pravimo, da je relacija refleksivna, ker velja, da vsako število deli samega sebe.
Velja: 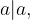 ker
ker 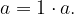
Pravimo, da je relacija antisimetrična, ker velja, da če dve števili delita drug drugega, potem sta števili enaki.
Če 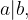 in
in 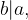 potem je
potem je 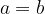
Pravimo, da je relacija tranzitivna, ker velja, da ko neko število 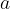 deli število
deli število 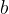 ter to isto število
ter to isto število 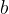 deli število
deli število  , tedaj število
, tedaj število 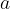 deli tudi število
deli tudi število  .
.
Če 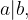 in
in 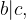 potem
potem 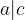 .
.
Definicijo deljivosti lahko razširimo na cela števila. Naj bosta 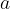 in
in 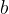 celi števili. Število
celi števili. Število 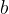 deli število
deli število 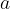 , če obstaja tako celo število
, če obstaja tako celo število 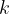 , da velja
, da velja
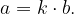
Velja tudi, da je 0 deljivo z vsakim neničelnim celim številom 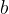 , saj je
, saj je
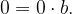
Vsako celo število 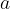 ima najmanj 4 delitelje:
ima najmanj 4 delitelje:
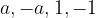
Naj bosta 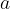 in
in 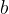 naravni števili. Vedno velja, da sta vsota
naravni števili. Vedno velja, da sta vsota
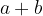
ter produkt
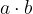
naravni števili, kvocient oziroma količnik pa ni nujno naravno število. Kadar je kvocient naravno število vemo, da sta števili 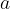 in
in 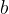 v relaciji deljivosti, sicer pa nista v relaciji in nam pri deljenju ne vrneta naravnega števila.
v relaciji deljivosti, sicer pa nista v relaciji in nam pri deljenju ne vrneta naravnega števila.
Ne glede na dejstvo, ali sta dve naravni števili v relaciji deljivosti ali pa ne, lahko za vse pare naravnih števil 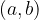 , kjer je
, kjer je 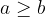 , zapišemo osnovni izrek o deljenju.
, zapišemo osnovni izrek o deljenju.
Osnovni izrek o deljenju pravi, da deljenje poljubnih dveh naravnih števil 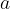 in
in 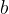 , za katera velja
, za katera velja 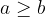 in
in 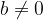 , lahko zapišemo kot
, lahko zapišemo kot
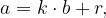
kjer je:
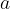 deljenec
deljenec
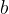 delitelj
delitelj
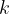 kvocient oziroma količnik
kvocient oziroma količnik
 ostanek, kjer
ostanek, kjer  .
.