Osebne zbirke


Vektorje že poznamo. Poglejmo si, kdaj so vektorji kolinearni in komplanarni ter kaj je baza ravnine in prostora.
Vektorja 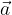 in
in 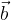 sta kolinearna, če sta vzporedna oziroma ležita na vzporednih nosilkah premic.
sta kolinearna, če sta vzporedna oziroma ležita na vzporednih nosilkah premic.
Če sta vektorja 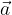 in
in 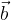 kolinerana in je
kolinerana in je 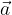 različen od nič, potem obstaja tak
različen od nič, potem obstaja tak 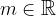 , da velja:
, da velja:
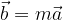
Trije vektorji so komplanarni, če ležijo v isti ravnini.
Če so vektorji 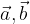 in
in 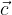 komplanarni, potem obstajata tak
komplanarni, potem obstajata tak 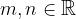 , da velja:
, da velja:
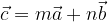
Linearna kombinacija vektorjev je navadna vsota več različnih vektorjev, pomnoženih s poljubnimi realnimi števili.
Linearna kombinacija vektorjev 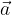 in
in 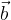 je vsak izraz zapisan kot vsota teh dveh vektorjev, pomnoženih s poljubnima realnima številoma k in l:
je vsak izraz zapisan kot vsota teh dveh vektorjev, pomnoženih s poljubnima realnima številoma k in l:
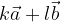
Rezultat linearne kombinacije so različni vektorji, odvisni od danih vektorjev in vrednosti realnih števil. Za realni števili k = l = 0 in dana vektorja 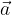 in
in 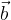 dobimo kot rezultat ničelni vektor:
dobimo kot rezultat ničelni vektor:
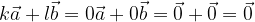
Takšne vektorje, pri katerih je njihova linearna kombinacija ničelni vektor samo v primeru, ko je k = l = 0, imenujemo linearno neodvisni sicer ssta vektorja linearno odvisna. Intuitivno: vektorja sta linearno odvisna če sta vzporedna, sicer sta linearno neodvisna.
Vektorja 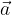 in
in 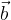 sta linearno neodvisna, če lahko za poljubna k in l njuno vsoto
sta linearno neodvisna, če lahko za poljubna k in l njuno vsoto
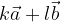
seštejemo v 0 če in samo če sta hkrati k = 0 in l = 0. Sicer sta vektorja linearno odvisna.
Vektorja 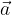 in
in 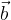 sta linearno odvisna, če in samo če sta kolinearna.
sta linearno odvisna, če in samo če sta kolinearna.
Linearna kombinacija vektorjev 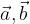 in
in 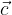 je vsak izraz zapisan kot vsota teh treh vektorjev, pomnoženih s poljubnimi realnima števili k, l in m:
je vsak izraz zapisan kot vsota teh treh vektorjev, pomnoženih s poljubnimi realnima števili k, l in m:
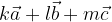
Rezultat linearne kombinacije so različni vektorji, odvisni od danih vektorjev in vrednosti realnih števil. Za realna števila k = l = m = 0 in dane vektorje 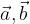 in
in 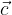 dobimo kot rezultat ničelni vektor:
dobimo kot rezultat ničelni vektor:
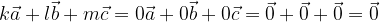
Takšne vektorje, pri katerih je njihova linearna kombinacija ničelni vektor samo v primeru, ko je k = l = m = 0, imenujemo linearno neodvisni, sicer so vektorji linearno odvisni. Intuitivno: vektorji so linearno odvisni če so komplanarni, sicer so linearno neodvisni.
Vektorji 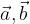 in
in 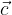 so linearno neodvisni, če lahko za poljubne k, l in m njuno vsoto
so linearno neodvisni, če lahko za poljubne k, l in m njuno vsoto
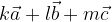
seštejemo v 0 če in samo če so hkrati k = 0, l = 0 in m=0. Sicer so vektorji linerano odvisni.
Vektorji 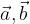 in
in 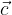 so linearno odvisni, če in samo če so komplanarni.
so linearno odvisni, če in samo če so komplanarni.
Sedaj pa poglejmo:
kaj predstavljata vektorja, ki nista vzporedna (pravimo, da sta linearno neodvisna oziroma nekolinearna) in
kaj predstavljajo vektorji, ki ne ležijo v isti ravnini (so linearno neodvisni oziroma nekomplanarni).
Bazo ravnine določata dva neničelna, nevzporedna (nekolinearna vektorja) 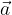 in
in 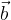 , s katerima lahko vse preostale vektorje v ravnini izrazimo na en sam način, kot linearno kombinacijo teh dveh vektorjev:
, s katerima lahko vse preostale vektorje v ravnini izrazimo na en sam način, kot linearno kombinacijo teh dveh vektorjev:
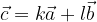
pri čemer sta 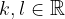 .
.
Zapis vektorja (npr. 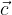 ) po bazi vektorjev (npr.
) po bazi vektorjev (npr. 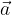 in
in 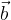 ) pravimo razvoj vektorja po bazi.
) pravimo razvoj vektorja po bazi.
Bazo prostora določajo trije neničelni vektorji 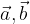 in
in 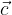 , ki ne ležijo v isti ravnini in s katerimi lahko vse preostale vektorje v prostoru izrazimo na en sam način, kot linearno kombinacijo teh treh vektorjev:
, ki ne ležijo v isti ravnini in s katerimi lahko vse preostale vektorje v prostoru izrazimo na en sam način, kot linearno kombinacijo teh treh vektorjev:
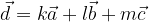
pri čemer sta
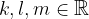
Zapis vektorja (npr. 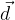 ) po bazi vektorjev (npr.
) po bazi vektorjev (npr. 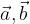 in
in 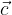 ) pravimo razvoj vektorja po bazi.
) pravimo razvoj vektorja po bazi.
Vektorje, ki določajo bazo ravnine oz. prostora, imenujemo bazni vektorji, realna števila, ki nastopajo v razvoju vektorja po bazi, pa imenujemo komponente.
Število baznih vektorjev je določeno z dimenzijo prostora. Ker je ravnina 2-dimenzionalna, tvorita bazo ravnine dva vektorja in ker je prostor 3-dimenzionalen, tvorijo bazo prostora trije vektorji.
Baza je ortogonalna, če so bazni vektorji pravokotni drug na drugega; normirana, če so vektorji enotski (imajo dolžino ena) in ortonormirana, če so vektorji enotski in med seboj pravokotni.