Osebne zbirke


Luka prime za ročaj vozička in ga vleče po klancu navzgor. Voziček je težak in Luka se le stežka pomika naprej. Zato na pomoč pokliče prijatelja Jana. Sedaj gre lažje in voziček brez posebnega napora povlečeta na vrh klanca.
Luka in Jan sta delovala na voziček vsak s svojo silo. Obe vlečni sili sta se sešteli, zato je bil skupen učinek sil na voziček večji, kot če bi vlekel Luka sam.
Poglejmo še en primer, ko na eno telo delujeta dve sili v različnih smereh.
Vidimo, da se sile, ki skupaj delujejo na neko telo, seštejejo in povzročajo na njem skupen učinek. V nadaljevanju si poglejmo, kaj je rezultat seštevanja sil in kako sile seštejemo.
Ko na telo deluje več sil hkrati, jih lahko seštejemo. Kot rezultat seštevanja dobimo silo, ki ji pravimo vsota sil ali z eno besedo: rezultanta. Z njo nadomestimo vse sile, ki so prej delovale na telo.
Rezultanta je torej sila. Kot vsako silo lahko tudi rezultanto predstavimo z usmerjeno daljico. Določili ji bomo:
smer s pomočjo puščice in
velikost s pomočjo merila.
Rezultanta je vsota vseh sil, ki delujejo na neko telo. To je ena sama sila, s katero nadomestimo vse druge sile. Njen učinek na gibanje telesa je enak, kot učinek vseh sil skupaj.
Poglejmo si še, kako seštevamo sile. Drugače je, če sile delujejo v istih smereh ali različnih smereh. Zato bomo pri določanju rezultante obravnavali naslednje primere:
sile delujejo na telo vzporedno, v isti smeri,
sile delujejo na telo vzporedno, v nasprotni smeri,
sile delujejo na telo v različnih smereh.
Vzporedne sile, ki delujejo na telo, imajo lahko isto ali nasprotno smer:
V vseh primerih vzporednih sil lahko rezultanto dobimo z:
grafičnim seštevanjem sil in
računskim seštevanjem sil.
Obema metodama se podrobneje posvetimo v nadaljevanju.
Vsoto ali rezultanto vzporednih sil lahko dobimo na dva načina:
z grafičnim seštevanjem sil,
z računskim seštevanjem sil.
Če na telo deluje več sil v isto smer, potem se njihov skupni učinek poveča. Učinek je tak, kot bi na telo delovali z eno silo, ki ima velikost vseh sil skupaj.
Poglejmo si grafični in računski postopek seštevanja sil. Oba postopka bomo pogledali na primeru dveh sil. Če je sil več, pa po enakem zgledu seštejemo vse sile.
Grafični postopek seštevanja sil
Sili seštejemo tako, da:
Sili najprej narišemo v prijemališčih, na katerih dejansko delujejo na telo.
Nato sili vzporedno premaknemo iz slike. Natovorimo ju drugo na drugo tako, da prijemališče druge sile vzporedno premaknemo na konico prve sile.
Povežemo začetek prve sile s konico druge sile.
Dobimo rezultanto obeh sil:
prijemališče ima v prijemališču prve sile,
puščico pa na puščici druge sile.
Poljubno lahko izberemo katera sila je prva in katera druga.
Računski postopek določanja rezultante
Sili delujeta vzporedno in v isti smeri, zato lahko dobimo rezultanto tudi tako, da velikosti sil seštejemo. Rezultanta kaže v isto smer, kot obe sili.
Ko na telo delujeta sili v nasprotnih smereh, si tudi njuna učinka nasprotujeta. To je tako, kot bi na telo delovala ena sila, ki ima velikost razlike obeh sil. Pravimo, da se sili odštejeta.
Poglejmo si grafični in računski postopek seštevanja sil, ki delujeta v nasprotno smer.
Grafično seštevanje sil, ki delujeta v nasprotno smer
Sili seštejemo, tako da:
Najprej sili narišemo v prijemališčih, na katerih dejansko delujeta na telo.
Nato sili vzporedno premaknemo in ju natovorimo drugo na drugo. Začetek druge sile postavimo na konico prve sile. Pri tem upoštevamo, da je smer druge sile nasprotna smeri prve.
Dobimo rezultanto sil:
prijemališče ima v prijemališču prve sile,
puščico pa na puščici druge sile.
Računski postopek
Sili delujeta vzporedno in v nasprotni smeri. Zato lahko dobimo rezultanto tudi tako, da sili številsko odštejemo. Rezultanta kaže v smer večje sile.
Dve sili sta nasprotno enaki, če sta:
enako veliki in
nasprotno usmerjeni.
V tem primeru se izničita (odštejeta). Njuna rezultanta je enaka nič, telo se zato ne premakne.
Ko računamo vsoto dveh nasprotnih sil, jima dodelimo pozitivni in negativni predznak, na primer:
sila, usmerjena na desno, ima pozitivni predznak,
sila, usmerjena v levo, ima negativni predznak.
Sili na na zgornji sliki sta enako veliki, a nasprotno usmerjeni. Njuna vsota ali rezultanta je zato enaka nič:
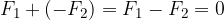
Učinek obeh sil na gibanje telesa je enak, kot če nanj ne bi delovala nobena sila.
Če sta sili enako veliki in nasprotno usmerjeni, je njuna vsota ali rezultanta enaka nič.
Nevzporedne sile delujejo na telo v različnih smereh. Prijemališče nevzporednih sil ni nujno v isti točki. S seštevanjem takšnih sil prav tako dobimo rezultanto, ki nadomesti vse sile.
Velikost rezultante ni enaka seštevku velikosti vseh sil. Upoštevati moramo, da sile delujejo v različnih smereh. Njihove velikosti se zato ne seštejejo kot števila.
Nevzporedne sile seštevamo geometrijsko. Pri seštevanju sta možna dva postopka (pravili):
paralelogramsko pravilo ali
večkotnik sil
Pri obeh postopkih uporabimo vzporedne premike sil in dobimo enako rezultanto.
Pri seštevanju nevzporednih sil uporabimo paralelogramsko pravilo ali pa tvorimo večkotnik sil, oboje z vzporednim premikanjem sil.
To pravilo večinoma uporabljamo pri seštevanju dveh nevzporednih sil.
Postopek seštevanja sil po paralelogramskem pravilu je naslednji:
Sili vzporedno premaknemo v isto prijemališče. Dobimo dve stranici paralelograma.
Drugi dve stranici paralelograma dobimo z risanjem vzporednic skozi puščici prvih dveh sil.
Rezultanta je diagonala paralelograma s:
prijemališčem v isti točki, kot sta prijemališči obeh sil
in puščico v presečišču vzporednic.
Postopek si poglejmo na konkretnem primeru.
Ta postopek uporabimo, ko seštevamo dve ali več nevzporednih sil naenkrat.
Če seštevamo samo dve sili, temu postopku pravimo trikotniško pravilo, saj sili tvorita trikotnik. Običajno pa ta postopek uporabimo, ko seštevamo več nevzporednih sil. Takrat dobimo večkotnik sil.
Postopek seštevanja sil je tak, da sile vzporedno premikamo in jih natovarjamo drugo na drugo. To pomeni, da:
Na puščico prve sile vzporedno prenesemo prijemališče druge sile.
Na puščico druge sile vzporedno prenesemo prijemališče tretje sile in tako naprej do zadnje sile.
Rezultanta je usmerjena daljica, ki povezuje:
prijemališče prve sile in
puščico zadnje sile.
Postopek si bomo ogledali na konkretnem primeru.