Prijava z e-naslovom
Prijava brez gesla
Curek vode iz visokoležečega jezera brizga z veliko hitrostjo na lopatice kolesa Peltonove turbine (glej sliko 1, levo). Zaradi velike hitrosti je tudi sila curka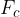 
na lopatice velika. Kolo se vrti s hitrostjo 
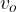in poganja npr. električni generator.
Lopatice Peltonove turbine so oblikovane tako, da se voda - po tem, ko odda energijo turbini - odbija nazaj v smer, od koder je delovala na turbino (glej sliko 1, desno). Zakaj je to potrebno, bomo spoznali v naslednjem poglavju.
Slika 1: sila curka vode na Peltonovo turbino.
Ko govorimo o sili curka, mislimo pri tem na silo curka poljubne tekočine: vode ali plina (npr. zraka).
Kaj pa je fizikalno ozadje sile, s katero deluje curek na telo in telo nazaj na curek?
Gibajoča voda ima svojo maso in hitrost. Ima torej gibalno količino. Ko zadene ob oviro se lahko od ovire odbije kot v primeru Peltonove turbine ali pa izgubi celotno gibalno količino in se odcedi na tla. V obeh primerih je delovala ovira na curek (ali pa curek na oviro - glej Vzajemno delovanje sil) in ji spremenila gibalno količino.
Curek si lahko predstavljamo kot volumenski tok snovi. Vzemimo npr. valjast odsek takega curka. Zamislimo si osnovno ploskev S, ki se giblje skupaj s curkom (glej sliko 2). V času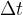 
naredi presek S pot 
. Pri tem presek S opiše volumen 
.
Slika 2: volumenski tok.
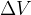Volumenski tok definiramo kot spremembo volumna (ali pretečen volumen) v opazovanem času:
Volumenski tok je prirastek volumna v opazovanem času:
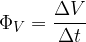
Izračunamo ga lahko, če poznamo tokovni presek S in hitrost gibanja toka v:
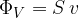
Če nas je v predhodnem poglavju zanimal:
volumen, ki ga opiše tok v danem času,
nas bo zdaj zanimala:
masa ki se pretoči v danem času.
Naj se po valjasti cevi giblje neka masa. Masni tok definiramo kot razmerje med:
maso, ki gre skozi opazovani presek cevi v opazovanem času in
opazovanim časom.
Zapišimo razmerje:
Masni tok pove, koliko mase neke snovi steče mimo v določenem času:
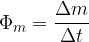
Izrazimo ga lahko z volumenskim tokom in gostoto snovi:
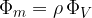
ali pa z gostoto snovi, presekom curka in hitrostjo:
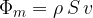
Vzemimo curek, ki teče po cevi s presekom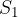 
s hitrostjo 
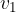. Cev se postopno zoži na presek 
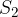. Da bo pretekel enak volumen snovi v istem času v obeh delih cevi pričakujemo, da se bo morala snov v ožjem delu gibati hitreje kot v širšem.
Stacionarni tok je tok, ki ima vedno enak volumenski pretok, ne glede na to, kje ga merimo.
Če je tok stacionaren, mora biti volumenski tok v obeh delih cevi enak:
V primeru stacionarnega toka je produkt preseka skozi curek in hitrosti konstanten:
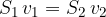
Curek zadene oviro in se od nje odbije. Ovira je delovala na curek s sunkom sile tako, da mu je spremenila gibalno količino. Opazujmo sunek sile na majhno maso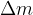 
, ki je bila v stiku z oviro čas :
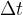Zaradi vzajemnega delovanja sil deluje curek na oviro z nasprotno enako silo:
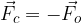
Sila curka je produkt masnega toka in razlike hitrosti po trku in pred trkom:
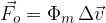
kjer je:
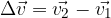
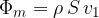
Sila curka je nasprotna sili, s katero deluje ovira na curek:
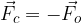
Curek masnega toka izhaja iz šobe. V skladu z vzajemnim delovanjem sil sila, ki je nasprotna sili curka deluje na samo šobo tako, da jo potiska v nasprotno smer, kot je hitrost curka. Sili pravimo reakcijska sila.
Vzemimo, da iz šobe izhaja masni tok s hitrostjo v. Reakcijska sila je:
Reakcijska sila je usmerjena v nasprotno smer gibanja toka in je produkt masnega toka in hitrosti curka:
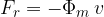
Če iz telesa izhaja curek snovi z gostoto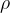 
, presekom S in hitrostjo v izračunamo reakcijsko silo po enačbi:
