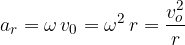Osebne zbirke


V gradivu Sila kot vektor smo se naučili, da sila lahko:
spremeni hitrost gibanja telesa in / ali
spremeni smer gibanja telesa in / ali
telo deformira.
Ko telo kroži, očitno spreminja smer gibanja. V tem gradivu nas bo zanimalo, katere sile povzročajo to spremembo in kaj se med enakomernim kroženjem dogaja.
V gradivu Enakomerno kroženje smo se osredotočali predvsem na gibanje telesa, njegova masa pa nas ni zanimala. Kaj pa, če upoštevamo, da telo ima maso?
Če pa telo ima maso in je gibanje obenem pospešeno, imamo opravka, skladno z 2. Newtonovim zakonom, s silo. Silo izračunamo z:

Ker masa ni vektor in nima smeri, je smer sile določena s smerjo pospeška. In kot smo ugotovili v gradivu Enakomerno kroženje, je pospešek, ki povzroča spremembo smeri gibanja, radialni pospešek. Radialni pospešek je pravokoten na vektor obodne hitrosti in kaže proti središču krožnice (glej sliko 2). V to smer bo kazala tudi sila, ki ji pravimo radialna sila ali centripetalna sila.
Da jasno naznačimo, da govorimo o radialni sili in radialnemu pospešku, enačbo za silo opremimo z indeksom r:
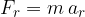
Iz gradiva Enakomerno kroženje vemo, da lahko radialni pospešek zapišemo v več različnih oblikah:
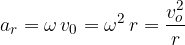
Vsako izmed enačb lahko vstavimo v enačbo za radialno silo. Dobimo:
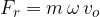
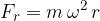
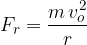
Vzroki za radialno silo so lahko zelo različni. Naštejmo jih nekaj:
Radialno silo lahko omogoča sila sila lepenja med telesom in podlago (primer avtomobila v ovinku v uvodu).
Kroženje telesa na vrvici v vodoravni ravnini omogoča radialna sila, ki je enaka sili vrvice, na katero je obešeno krožeče telo.
Kroženje Meseca okoli Zemlje omogoča gravitacijska sila med Zemljo in Mesecem.
Radialna sila je lahko rezultanta večih sil (npr. sila vrvice in gravitacijska sila; primer je podan nekoliko nižje).
Telo z maso m kroži zaradi radialne sile, ki ga sili v kroženja. V kolikor je več sil, ki vplivajo na kroženje, velja: rezultanta vseh sil, ki delujejo na telo, ki kroži, je enaka radialni sili. Radialno silo izračunamo s pomočjo zakona dinamike:
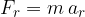
Radialni pospešek izračunamo z eno izmed enačb: