Osebne zbirke


Za uvod v gradivo si oglejmo dva primera.
Spoznali smo dve vrsti simetrije:
prtiček iz prvega primera je osno simetričen,
mavrični krog iz drugega primera pa je središčno simetričen.
Oglejmo si ju še nekoliko podrobneje.
Določene predmete lahko s pomočjo navidezne črte razdelimo na dva dela, ki se popolnoma prekrivata. Predmet s takšno lastnostjo je osno simetričen. Navidezno črto, ki ga razpolavlja, pa imenujemo simetrala.
V naravi najdemo veliko primerov osne simetrije:
Osno simetrijo lahko ugotavljamo tudi s pomočjo zrcala.
Simetrijo lahko opazujemo tudi pri geometrijskih likih.
Lik ima lahko več simetral, lahko pa nima nobene. Na spodnji sliki je nekaj geometrijskih likov z vrisanimi simetralami:
Osna simetrija je tesno povezana z zrcaljenjem preko premice.
Lik je osno simetričen, če obstaja takšna premica, preko katere se lik preslika sam vase.
Premico, preko katere se lik preslika sam vase, imenujemo simetrala oziroma somernica.
Vsi pravilni mnogokotniki so simetrične oblike. Število simetral je enako številu njegovih stranic.
Če obstaja točka, preko katere se lik preslika sam vase, je lik središčno simetričen.
Središčna simetrija je v tesno povezana z zrcaljenjem preko točke.
Lik je središčno simetričen, če obstaja točka T, preko katere se lik preslika sam vase.
Točko, preko katere se lik preslika sam vase, imenujemo središče simetrije.
Če se vsaj ena točka na liku preko točke T ne preslika nazaj na lik, potem lik ni središčno someren.
Nekateri liki so hkrati osno in središčno simetrični.
Lik, ki je hkrati osno in središčno simetričen, ima središče simetrije v presečišču simetral.
Središčno simetrijo lahko ugotovimo tudi tako, da lik zavrtimo za 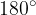 okoli središča simetrije. Če dobimo popolnoma enako sliko kot pred zasukom, je lik središčno simetričen.
okoli središča simetrije. Če dobimo popolnoma enako sliko kot pred zasukom, je lik središčno simetričen.