Osebne zbirke


V nadaljevanju si bomo sklepni in procentni račun pogledali ločeno:
Sklepni račun srečujemo v vsakdanjem življenju (stiskanje sokov, gradnja hiše,...). Pri problemih iz sklepnega računa se ponavadi pojavljata dve količini, ki sta v enostavni medsebojni zvezi. Ta zveza je lahko:
premo sorazmerna
obratno sorazmerna
Oglejmo si obe zvezi natančneje.
Količini sta premo sorazmerni, kadar:
eno količino povečamo (zmanjšamo) za 2-krat, 3-krat,...
se hkrati druga količina poveča (zmanjša) za 2-krat, 3-krat,...
Količini sta obratno sorazmerni, kadar:
eno količino povečamo (zmanjšamo) za 2-krat, 3-krat,...
se hkrati druga količina zmanjša (poveča) za 2-krat, 3-krat,...
Tudi procentni račun srečujemo v vsakdanjem življenju (podražitve, pocenitve,...). Največkrat nas zanima kakšen je relativni delež:
Velikokrat želimo povedati, kako velik del celote predstavlja določen delež. To razmerje imenujemo relativni delež:
Vsak relativni delež pa lahko zapišemo tudi s pomočjo procentov.
Rezultat relativnega deleža lahko zapišemo kot ulomek, lahko pa ga zapišemo tudi v odstotkih oziroma procentih.
To najlažje storimo z naslednjim obrazcem:
Splošni obrazec za procentni račun:
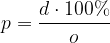
kjer d predstavlja del, o pa celoto.
Če s p označimo število odstotkov (procentov), potem v splošnem velja:
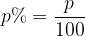
Zgornji obrazec si poglejmo na naslednjem primeru:
Med zapisom s procenti in relativnim deležem obstaja povezava.
Najprej zapišimo relativni delež:
Odstotke (procente) lahko tako izrazimo z relativnim deležem: