Prijava z e-naslovom
Prijava brez gesla
Ko množico podatkov grupiramo in grafično predstavimo, se vprašamo tudi, ali obstaja neka tipična vrednost s katero bi opisali celotno množico podatkov naenkrat. Taki tipični vrednosti rečemo parameter. Parametrov je v statistični raziskavi lahko več, eden najpomembnejših je srednja vrednost.
Srednjih vrednosti je več vrst, v tem gradivu bomo spoznali naslednje:
aritmetično sredino;
modus;
mediano.
Aritmetični sredini pravimo tudi povprečna vrednost. Povprečna vrednost je [vsota vseh statističnih spremenljivk] deljeno s [številom vseh vrednosti]:
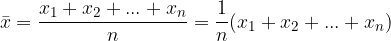
kar lahko krajše zapišemo kot:
V primeru, da se vrednosti statistične spremenljive ponavljajo (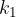
vrednosti 
, 
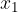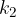vrednosti 
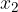, itd..), srednjo vrednost izračunamo po enačbi, ki nam računanje nekoliko pohitri:
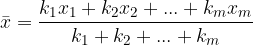
Obe enačbi za izračun srednje vrednosti sta ekvivalentni. To pomeni, da ne glede na to, katero enačbo uporabimo, bomo vedno dobili isto vrednost aritmetične sredine.
Aritmetična sredina je zelo občutljiva za ekstremne vrednosti ali osamelce, še posebej, če ležijo le na eni strani množice podatkov. V takem primeru se aritmetična sredina pomakne v tisto smer, in to tem bolj, čim bolj oddaljen je osamelec.
V primeru, da smo podatke grupirali, aritmetično sredino izračunamo tako:
Najprej za vsak frekvenčni razred izračunamo njemu lastno aritmetično sredino.
Nato pa izračunamo povprečje vseh (pod točko 1. izračunanih) aritmetičnih sredin frekvenčnih razredov.
Z grupiranjem podatkov izgubimo določeno informacijo in je zato aritmetična sredina le približno izračunana.
Modus ali gostiščnica (oznaka: Mo) je tista vrednost, ki se v množici vseh vrednosti najpogosteje ponavlja.
Modus v diskretnih podatkih je enak podatku, ki se največkrat pojavlja.
Ob majhnem številu diskretnih podatkov je modus ponavadi zavajajoča srednja vrednost.
V primeru, da imamo podatke grupirane, namesto modusa poiščemo modalni razred: to je tisti razred, ki ima največjo frekvenčno gostoto.
Vrednost modusa ni nujno vedno enolično določena. Zgodi se lahko, da se dve vrednosti pojavijo enako pogosto. Če se to zgodi, pravimo, da je porazdelitev vrednosti bimodalna.
Zgodi se lahko tudi, da se več vrednost pojavi enako pogosto. To imenujemo polimodalnost.
Mediana ali središčnica (oznaka: Me) je tista vrednost statistične spremenljivke, pri kateri je polovica vrednosti manjših ali enakih, druga polovica pa večjih od nje.
Mediana predstavlja vrednost, ki predstavlja srednji podatek. Izračunamo jo kot:
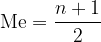
V primeru sodega števila podatkov ugotovimo, da ni pravega srednjega podatka. Za vrednost mediane v tem primeru vzamemo aritmetično sredino srednjih dveh podatkov.
Mediana je od vseh srednjih vrednosti najmanj občutljiva za osamelce in ponavadi dobro predstavlja opazovano množico. Posebno lahko jo je izračunati, če so podatki že urejeni po velikosti (rečemo tudi, da so podatki rangirani).
